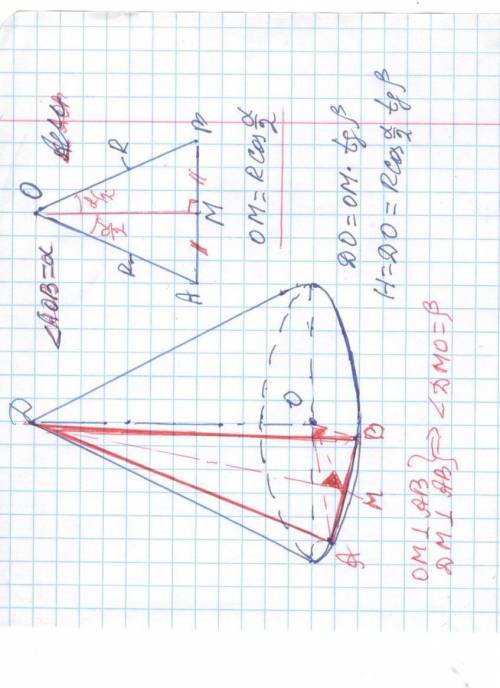
Плоскость, проведённая через две образующие ( DA и DB ) конуса,пересекает его основания по хорде, которая видна из центра основания конуса под углом α. Угол между проведённой плоскостью и плоскостью основания конуса равен β Найдите объем конуса, если радиус его основания равен R.
Дано:
DA и DB →образующие→ ;
OA = OB = R ; DO⊥ пл. осн || DO⊥ ( пл. круга ) ||
∠AOB = α ; β = (DAB) ^ (пл. осн)
- - - - - - -
V -?
Решение : V = (1/3)S*H = (1/3)πR²*DO
В равнобедренном треугольнике AOM (OA =OB = R ) из вершины O проведем медиану OM и точка M соединим с D _вершиной конуса . OM одновременно и высота OM ⊥ AB и биссектриса ∠AOM = ∠BOM =(1/2)∠AOB = α/2 .
В треугольнике ΔAOM : OM =Rcos(α/2)
ΔDAB тоже равнобедренный DA =DB (образующие), следовательно медиана DM одновременно и высота DM ⊥ AB .
DM ⊥ AB и OM ⊥ AB ⇒ ∠DMO =β ( линейный угол)
Из ΔDOM : DO = OM*tgβ =Rcos(α/2)*tgβ ; H =DO
V =(1/3)πR²*H =(1/3)πR²*Rcos(α/2)*tgβ =(1/3)cos(α/2)*tgβ πR³
ответ: V = (1/3)cos(α/2)*tgβ πR³ ед. объема
Объяснение:
Пусть радиус основания цилиндра х, тогда высота цилиндра (х+12) см.
В осевом сечении цилиндра-прямоугольник⇒х(х+12)=90.
х²+12х-90=0 , Д=в²-4ас, Д=144+4*90=504=36*14
х₁=(-в+√Д):2а , х₁=(-12+6√14):2=-6+3√14=3√14-6>0 , т.к.3√14=√126, √126>√36.
х₂=(-в-√Д):2а , х₂=(-12-6√14):2.=-6-3√14 не подходит по смыслу задачи.
r=3√14-6 , h=12+3√14-6=6+3√14.
V=S(осн)*h.
S(осн)=Пr², S(осн)=П(3√14-6)²
V= П(3√14-6)² *(6+3√14)=П(3√14-6)² *(3√14+6)=П(3√14-6)*(3²√14²-6²)=
=П(3√14-6)*(126-36)=90П(3√14-6) (см²)
1. КОЛЛИНЕАРНЫМИ векторами называются такие вектора, которые лежат на одной или параллельных прямых(вектора не должны быть нулевыми) 2 два вектора называются противоположно если соблюдаеются 2 условия 1)модуль a равен модулю b 2)направление векторов разное 3Чтобы из одного вектора вычесть другой вектор(назовем их a и b) надо к вектору a прибавить вектор, противоположный вектору b. Полученный вектор и будет разностью векторов a и b (исправил,вроде правильно.)