(МН·РН) = 4 ед.
(ОР·РК) = -2 ед.
Объяснение:
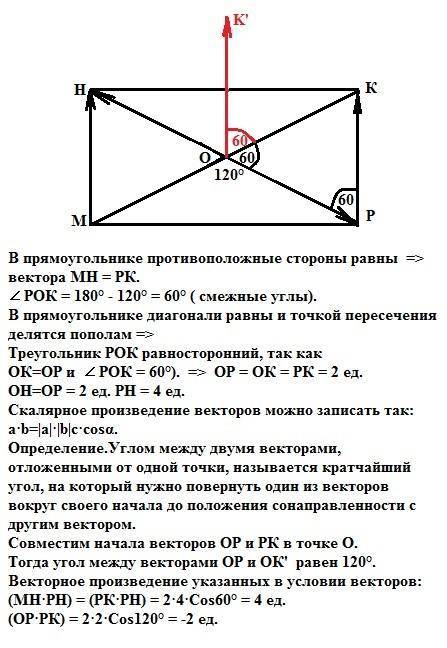
В прямоугольнике противоположные стороны равны =>
вектора МН = РК.
∠ РОК = 180° - 120° = 60° ( смежные углы).
В прямоугольнике диагонали равны и точкой пересечения делятся пополам =>
Треугольник РОК равносторонний, так как
ОК=ОР и ∠ РОК = 60°). => ОР = ОК = РК = 2 ед.
ОН=ОР = 2 ед. РН = 4 ед.
Скалярное произведение векторов можно записать так:
a·b=|a|·|b|c·сosα.
Определение: "Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором".
Совместим начала векторов ОР и РК в точке О. Тогда угол между векторами ОР и ОК' (вектора ОК и ОК' равны) равен 120°.
Векторное произведение указанных в условии векторов:
(МН·РН) = (РК·РН) = 2·4·Cos60° = 4 ед.
(ОР·РК) = 2·2·Cos120° = -2 ед.
№1. Дан отрезок АВ. Постройте его середину - точку С.
1. Построить отрезок АВ.
2. Провести окружность с центром в точке А с радиусом > половины отрезка АВ.
3. Провести окружность с центром в точке В с тем же самым радиусом, что и первая окружность.
4. Соединить точки пересечения этих окружностей прямой, которая пересекает отрезок АВ ровно ПОСЕРЕДИНКЕ, т.е. в точке С.
№2.
На луче АВ постройте отрезок CD, равный АВ.
1. Построить луч АВ
2. ЦИРКУЛЕМ измерить отрезок АВ и построить окружность (А, АВ) - с центром в точке А=С, радиусом АВ.
3. Окружность (А, АВ) и луч АВ пересекутся в точке Д.