Обозначим катеты буквами а и в.
Тогда а+в=7
ав/2=6 - площадь прямоугольного треугольника.
Решаем систему уравнений:
а+в=7
ав/2=6
а+в=7
ав=12
а=7-в
(7-в)в=12
7в-в^2-12=0
в^2-7в+12=0
D=49-4*12=1
в1=(7+1):2=4 в2=(7-1):2=3
а1=7-4=3 а2=7-3=4
Итак, катеты равны 3 см и 4 см.
Найдём гипотенузу с: с=корень(3^2+4^2)=5(см)
ответ:5см
Можно не прибегая к вычислениям сказать, что если длина увеличивается в 8 раз, то площадь увеличивается в 8*8=64 раза, а объем увелиится в 8*8*8=512 раз.
Если вспомнить формулу объема пирамиды,то она равна
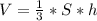
S - основание пирамиды, которое является правильным треугольником. Если его сторону увеличить в 8 раз, то исходный и полученный треугольники будут подобными как правильные треугольники. Только у получившегося треугольника сторона в 8 раз больше. По теореме о подобных треугольниках площадь у получившегося треуголника больше во столько же раз как и коэффициент подобия в квадрате, то есть в 8*8=64 раза.
h - высота пирамиды. Она тоже увеличиться в 8 раз, так как увеличивается ребро пирамиды и высота треугольника, являющегося в основании пирамиды. Ведь высота пирамиды получается из треугольника, где гипотенузой является ребро пирамиды (увеличено в 8 раз), катета, лежащего в основании пирамиды (это часть высоты треугольника в основании пирамиды от основания к точке пересечения высот треугольника). этот катет тоже увеличивается в 8 раз. Итого получается S - увеличен в 64 раза, h - в 8 раз. Значит обүем увеличился в 64*8=512 раз.
х+у=7
1/2ху=6
х+у=7
ху=12
х=7-у
(7-у)у=12
х=7-у
7у-у^2=12
y^2-7y+12=0
y1=3, у2=4
х1=4, х2=3
катеты 3 и 4