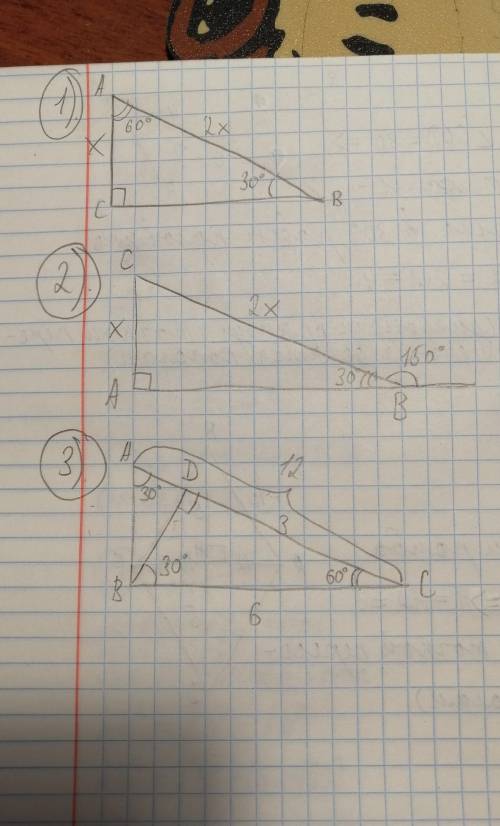
1). угол А = 90° - 30° = 60° => АВ - меньший катет (против меньшего угла меньшая сторона)
т. к. угол В = 30° => АС = 1/2 АВ (катет, лежащий против угла в 30°, равен половине гипотенузы)
Пусть АС = х, тогда АВ =2х
х+2х=36
3х=36
х=12, АВ=2*12=24
ответ: 12, 24
2). Угол СВА = 180°-150°=30° (сумма смежных углов равна 180°) => АС = 1/2 ВС (катет, лежащий против угла в 30°, равен половине гипотенузы)
Пусть АС = х, тогда СВ=2х
2х-х=10
х=10, СВ=2*10=20
ответ: 10, 20
3). Угол А = 30° => ВС = 1/2 АС = 6
Угол С = 90°-30°=60°
треуг. DBC - прямоуг., угол DВС = 90°-60°=30° => CD = 1/2 BC = 3
AD = 12-3=9
ответ: 3, 9
Радиус = 16
Объяснение:
И так начнём с формулы для радиуса. R= abc/(4*S)
Т.к. сумма углов треугольника = 180, а в равнобедренном треугольнике углы при основании равны, находим их:
(180-120)=30
Проводим высоту(она же медиана) и получаем два равных прямоугольных треугольника с гипотенузой 8 и углом 30;
Сторона которая лежит напротив угла 30 равна половине гипотенузы=>
Высота равнобедренного треугольника равна 4. Через cos(30) находим второй катет. sqrt(3)/2 = x/8=> x=2sqrt(3)
Находим основание . треугольника= 2sqrt(3)*2=4 sqrt(3)
Площадь же равна = (a*b*sin(120))/2 = 32*sin120= 32sqrt(3)/2
Подставляем всё в самую первую формулу
R= 8*8*4sqrt(3)/(32 sqrt(3)/2). Корень с трех сокращается и просто считаем. ответ 16
Уравнение прямой, проходящей через две точки (x1;y1) (x2;y2)^
(x-x1)\(x2-x1)=(y-y1)\(y2-y1)
(x-x1)\(x2-x1)*(y2-y1)+y1=y (если x1 не равно x2, y2 не равно y1)
Уравнение прямой AB
y=(x-2)\(-1-2)*(4-1)+1=2-x+1=-x+3
угловой коэфициент равен -1
Уравнение прямой AC
y=(x-2)\(3-2)*(-2-1)+1=6-3x+1=-3x+7
угловой коэфициент равен -3
Уравнение прямой BC
y=(x+1)\(3+1)*(-2-4)+4=-3\2x-3\2+4=-3\2x+5\2
угловой коэфициент равен -3\2
у перпендикулярных прямых произведение угловых коэфициентов равно -1
поэтому
угловой коээфициент высоты AH1, равен -1\(-3\2)=2\3
угловой коээфициент высоты BH2, равен -1\(-3)=1\3
угловой коээфициент высоты CH3, равен -1\(-1)=1
Уравнение прямой имеет вид y=kx+b
Ищем уравнение прямой, проходящей через высоту AH1, (она проходит через точку А)
1=2\3*2+b, b=-1\3
y=2\3x+1\3
Ищем уравнение прямой, проходящей через высоту BH2, (она проходит через точку B)
4=1\3*(-1)+b, b=13\3
y=1\3x+13\3
Ищем уравнение прямой, проходящей через высоту CH3, (она проходит через точку C)
-2=1*3+b, b=-5
y=x-5
ответ: уравнения прямых, проходящих через высоты AH1, BH2, CH3 соотвественно y=2\3x+1\3 ,y=1\3x+13\3 , y=x-5