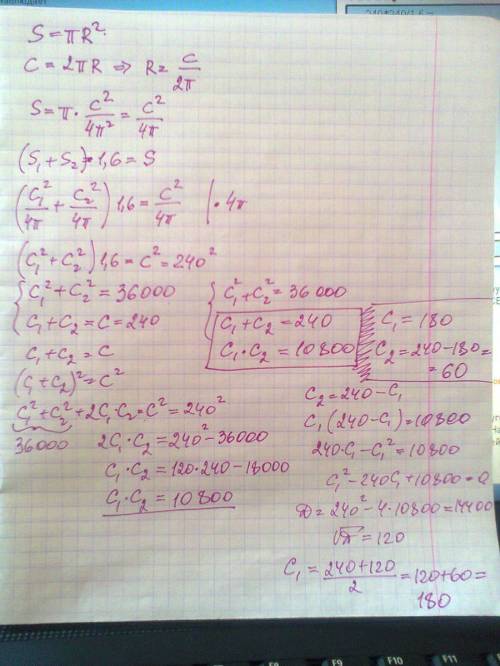находим боковую сторону трапеции: (52-8-18):2=13.
Высота трапеции равна корню квадратному из 13*13 -5*5=144 или это 12см (5 - длина отрезка, который отсекает высота от большего основания)
S=(8+18)/2 *12=13*12=156
2.
В
A D E C
Если ВД=ВЕ, то треугольник ДВЕ - равнобедренный. Угол ВДЕ=ВЕД. Отсюда угол ВДА=ВЕС как смежные углы (180-ВДЕ=180-ВЕД). Треугольники АВД и ВЕС равны по двум сторонам и углу между ними (АД=СЕ, ВД=ВЕ и угол ВДА=ВЕС). Значит АВ=ВС
пусть длина первого куска верёвки равна "x", второй-"y", а число пи обозначим как "p"
из условия задачи получаемсистему из двух уравнений:
1. x+y=240
2. p((x+y)/2p))^2=1.6(p(x-2p)^2+p(y/2p)^2)
уравнение 2 получается из условия задачи и следующих уравнений:
a) x=2pr, где "r" радиус окружности которая получается из веревки x
отсюда r=x/2p
b) y=2pt где, "t" радиус окружности которая получается из веревки y
отсюда t=x/2p
c) (x+y)/2p=n, где "n" радиус окружности которая получается из непорванной веревки
Решив систему уравнений состоящую из уравнений 1 и 2
найдём что длина первого куска верёвки либо 180м и тогда длина второго куска 60, либо длина первого куска верёвки 60м и тогда длина второго куска 180м