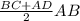 =
=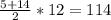 см²
см²
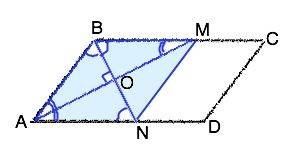
ВС|║АD, АВ - секущая. ⇒ сумма внутренних односторонних углов равна 180°. Биссектрисы делят углы пополам.⇒ из суммы углов треугольника угол ВОА=180°- 0,5•(∠АВС+∠ BAD)=90°,
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник ( для доказательства рассмотри накрестлежащие углы при секущих ВN и АМ) ⇒ ВМ=АВ, АN=AB ⇒ ВМ=АN. В ∆ ВМN отрезок ВО=ОN (т.к.в ∆ АВМ АО - медиана),⇒ МО - медиана и высота ( угол ВОМ =90° как смежный углу ВОА) ⇒ треугольник ВМN – равнобедренный и МN =ВМ Противоположные стороны четырехугольника АВMN равны и параллельны ( лежат на параллельных прямых), следовательно, АВMN– параллелограмм по определению. Кроме того, этот четырехугольник - ромб, т.к. все его стороны равны, а диагонали взаимно перпендикуляры и являются биссектрисами его углов. .
ответ: 2*sqrt(5). Пояснение: Выразим косинус угла между прямыми BA1 и BA2, при теоремы косинусов.Обозначим BA1=a , BA2=b , α=угол между BA1 и BA2 ,
тогда cos(α)=(a^2+b^2-64)/(2*a*b). После этого нужно выразить а и b через x. Для этого тоже воспользуемся теоремой косинусов (рассматривая треугольники BHA1 и BHA2 соответственно). Получим a^2=x^2-2*x+4 , b^2= x^2-10*x+100 . Эти значения подставим в выражение для косинуса альфы. Теперь подумаем, когда угол между прямыми максимальный? ответ: когда косинус принимает минимальное значение.
Теперь у нас есть выражение для cos(α) зависящее только от x ,и для получения ответа, нам нужно найти минимум этого выражения, то есть такой х , что выражение cos(α) минимально.
2))) Sтреугольника = a*h/2
причем, высоту можно проводить к любой стороне треугольника...
и поэтому становится интересен угол в 60 градусов --- ведь в прямоугольном треугольнике ему пара --- угол в 30 градусов...
а катет против угла в 30 градусов равен половине гипотенузы)))
(это уже начало синусов --- sin(30) = 1/2 ))))))
если проведем высоту к стороне 4V3 (((можно и к другой... рассуждения аналогичные, а ответ будет такой же... можно проверить...))), то
один из катетов получится = 6/2 = 3, а второй катет (как раз высоту...)))
можно найти по т.Пифагора: h^2 = 6^2 - 3^2 = (6-3)(6+3) = 3*9 = 27
S = 4V3 * V27 / 2 = 2*V3*V(3*9) = 2*3*3 = 18
1))) трапеция прямоугольная, => высота --- одна из ее боковых сторон...
если провести вторую высоту, то получим прямоугольный треугольник с гипотенузой = 5*h/4 ((( h : x = 4:5))) и катетом = (b-a) = 9
и по т.Пифагора можно записать: (5*h/4)^2 = h^2 + 9^2
25*h^2 / 16 - h^2 = 81
9*h^2 / 16 = 81
h^2 / 16 = 9
h^2 = 16*9
h = 4*3 = 12
меньшая диагональ (13) образует, в свою очередь, прямоугольный треугольник с меньшим основанием... 13^2 = a^2 + h^2
13^2 = a^2 + 16*9
a^2 = 13^2 - 12^2 = (13-12)(13+12) = 25
a = 5
тогда большее основание b = a+9 = 5+9 = 14
Sтрапеции = (5+14)*12 / 2 = 19*6 = 114