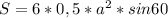, где а - сторона шестиугольника и любого из правильных треугольников. Зная площадь шестиугольника, мы находим, что 
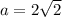. Каждая сторона шестиугольника стягивает дугу в 360\6= 60 градусов. А каждая сторона квадрата стягивает 360\4=90 градусов. Составим отношение: 60\а=90\б, где б - сторона квадрата. Выразим б. б=90а\60=
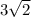. Площадь квадрата - это квадрат его стороны, поэтому его площадь будет равна 18.
1)уголА=80 градусов
В=100
С=80
D=100
2)уголB-уголA=30градусов
A=x ; B=x+30 ; A+B=x +x+30=2x+30 =180 ; x=75
A=75
B=105
C=75
D=105
3)угол А+уголC=140 градусов
A=C=140/2=70
A=70
B=110
C=70
D=110
4)уголB=2угла А
A=x ; B=2x ; A+B=x+2x=3x=180 ; x=60
A=60
B=120
C=60
D=120
5)уголABD=90градусов,уголADB=30ГРАДУСОВ - это треугольник
третий угол DAB = 180-90-30 =60 = A
A=60
B=120
C=60
D=120