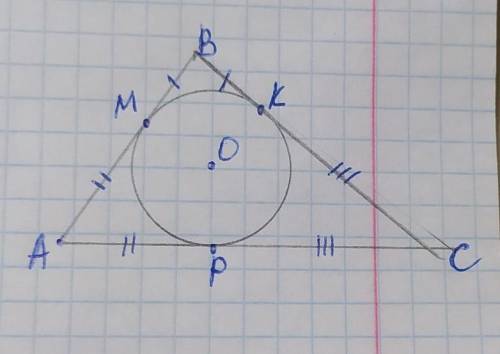
ВМ=1
ВК=1
АМ=4
АР=4
КС=6
РС=6
Объяснение:
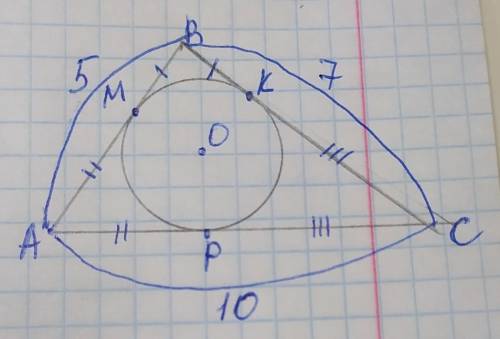
обозначим вершины треугольника А В С, точки касания М, К, Р, а центр вписанной окружности О. Стороны треугольника являются касательными к вписанной окружности, и отрезки касательных соединяясь в одной вершине равны от вершины до точки касания, поэтому: ВМ=ВК, АМ=АР, КС=РС. Пусть ВМ=ВК=х, тогда АМ=РМ=5–х, КС=РС=7–х. В этом случае сторона АС=АР+РС. Составим уравнение:
(5–х)+(7–х)=10
5–х+7–х=10
–2х+12=10
–2х=10–12
–2х= –2
х= –2÷(–2)
х=1
Итак: ВМ=ВК=1, тогда АМ=АР=5–1=4
КС=РС=7–1=6
Обе точки лежат на высоте треугольника, которая является одновременно и медианой и биссектрисой. Медиана делит высоту в соотношении 2:1, а биссектриса на части пропорциональные сторонам треугольника. Найдем высоту.
ВD = √AB²-AD² = √11²- 7² = 6√2
Медиана отсекает участок 6√2:3=2√2 от основания.
Биссектриса отсекает участок (7/18)*BD = (7/3)√2
Искомое расстояние (7/3)√2 - 2√2 = [(7-6)/3]√2 = (√2)/3 ≈ 0,47