P АВС=48 см.
Объяснение:
Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе.
sin A=CB÷AB.
Ни СВ, ни АВ нам не дано, поэтому необходимо найти такую тригонометрическую функцию, которая будет оперировать известной стороной АС.
2) Это самой функцией будет косинус. Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе.
cos A=АС÷АВ, где АС=12 см.
3) Найдём косинус, зная основное тригонометрическое тождество:
sin=√1-cos²α, откуда
cos=√1-sin²α.
За α примем ∠А. sin A=4/5=0,8. Итак:
cos=√1-sin²А.=√1-0,8²=√1-0,64=√0,36=0,6.
4) cos A=0,8=АС÷АВ=12÷АВ.
Через выражение 12÷АВ=0,6 можно выразить
АВ=12÷0,6=20 см.
5) Мы знаем АС=12 см и АВ=20 см, но не знаем ВС. Однако это исправимо, если воспользоваться Теоремой Пифгора:
АВ²=ВС²+АС², откуда можно выразить
ВС²=АВ²-АС²,
ВС²=20²-12²,
ВС²=400-144,
ВС²=256,
ВС=√256=16 см.
6) Периметром треугольника называют сумму длин его сторон.
Тогда Р ΔАВС=АВ+ВС+АС=20+16+12=48 см.
ответ: 12 см
Объяснение:
Обозначим данные три точки А, В и С. Они лежат на поверхности шара, следовательно, не лежат на одной прямой, и их можно объединить в треугольник АВС.
Отношение сторон треугольника АВС со сторонами 6:8:10=3:4:5 – это отношение сторон «египетского» треугольника => данный треугольник – прямоугольный, в котором наибольшая сторона гипотенуза АВ=10 см.
Расстояние от центра шара до вершин треугольника равно радиусу шара. => ∆ АВС вписан в окружность, по которой проходит сечение шара плоскостью.
По свойству окружности, описанной около прямоугольного треугольника, АВ является диаметром окружности в плоскости сечения шара.
Центр шара и центр окружности, в которую вписан ∆ АВС, лежат на одной прямой, при этом центр М окружности - середина гипотенузы ∆ АВС.
Расстоянием от точки О ( центра шара) до плоскости ∆ АВС является длина отрезка, проведенного от точки перпендикулярно плоскости.
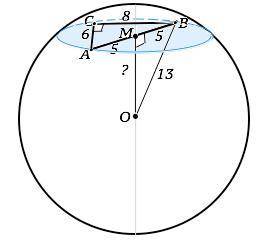
Рассмотрим схематический рисунок, сделанный согласно условиям задачи.
АВ - хорда, М - середина хорды. => ОМ⊥АВ (свойство радиуса) АМ=ВМ=5 см
∆ ОМВ - прямоугольный. Искомое расстояние ОМ=√(ОВ^2-ВМ^2)=√144=12 (см)