Окружность, описанная около треугольника
Окружность называется описанной около треугольника, если она проходит через все его вершины.
Теорема.
Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середины этих сторон.
Доказательство.
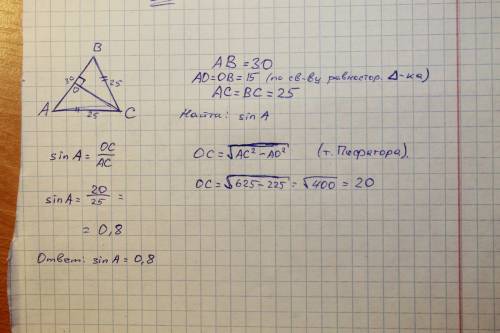
Пусть ABC – данный треугольник и O – центр окружности описанной около данного треугольника. Δ AOB – равнобедренный ( AO = OB как радиусы) . Медиана OD этого треугольника одновременно является его высотой. Поэтому центр окружности лежит на прямой, перпендикулярной стороне AC и проходящей через ее середину. Так же доказывается, что центр окружности на перпендикулярах к другим сторонам треугольника. Теорема доказана.
Объяснение:
С учётом, что дана правосторонняя система координат и положительное направление вращения против часовой стрелки относительно начала координат, формула новых координат имеет вид:
x' = x*cos α - y*sinα,
y' = x*sinα + y*cosα.
Подставив вместо х = а, вместо у = b, получим координаты точки при повороте:
- на 120 градусов.
c = a*cos 120 - b*sin120 = a*(-1/2) - b*(√3/2) ,
d = a*sin120 + b*cos120 = a*(√3/2) + b*(-1/2).
- на 240 градусов.
e = a*cos 240 - b*sin240 = a*(-1/2) - b*(-√3/2) ,
j = a*sin240 + b*cos240 = a*(-√3/2) + b*(-1/2).