В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой. Доказательство.Обратимся к рисунку, на котором АВС — равнобедренный треугольник с основанием ВС, АD — его биссектриса.Из равенства треугольников АВD и АСD (по 2 признаку равенства треугольников:AD-общая;углы 1 и 2 равны т.к. AD-биссектриса;AB=AC,т.к. треугольник равнобедренный) следует, что ВD = DC и 3 = 4. Равенство ВD = DC означает, что точка D — середина стороны ВС и поэтому АD — медиана треугольника АВС. Так как углы 3 и 4 смежные и равны друг другу, то они прямые. Следовательно, отрезок АО является также высотой треугольника АВС. Теорема доказана. В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой Если в треугольнике два угла равны, то он равнобедренный. Если в треугольнике медиана является и высотой, то такой треугольник равнобедренный.
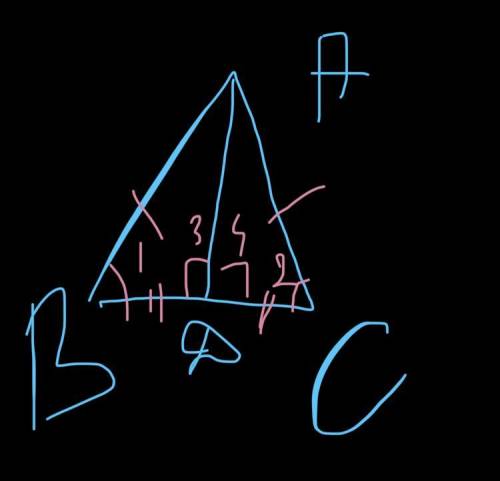
В равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.
Доказательство: Пусть ABC - равнобедренный треугольник (AC = BC), AK и BL - его медианы. Тогда треугольники AKB и ALB равны по второму признаку равенства треугольников. У них сторона AB общая, стороны AL и BK равны как половины боковых сторон равнобедренного треугольника, а углы LAB и KBA равны как углы при основании равнобедренного треугольника. Так как треугольники равны, их стороны AK и LB равны. Но AK и LB - медианы равнобедренного треугольника, проведённые к его боковым сторонам.
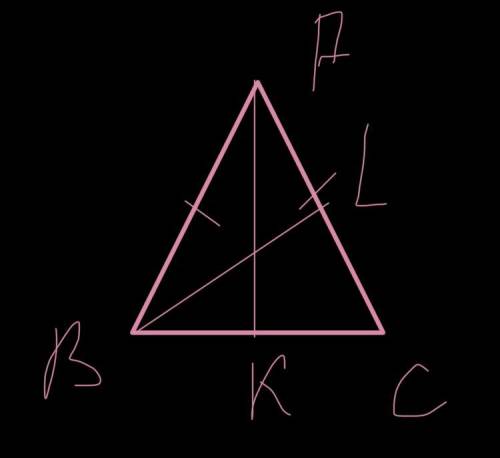
ответ: 135/7 см³
Объяснение:
Площадь боковой поверхности прямого параллелепипеда:
Sбок = Pосн · h
Pосн = (a + b) · 2 = (3 + 4) · 2 = 14 см
h = Sбок / Pосн = 15√3/14 см
Основание параллелограмм, его площадь:
Sосн = ab · sin60° = 3 · 4 · √3/2 = 6√3 см²
Объем:
V = Sосн · h = 6√3 · 15√3/14 = 135/7 см³