С2 ! 1- сторона ромба 20 см, одна из диоганалей 24 см . найдите длину второй диоганали . 2-диоганали ромба 18 см и 24 см . найдите периметр ромба и расстояния можду его паралельными сторонами .

👇

Ответ:

vanuhask12

20.03.2022

Дано: ромб АВСД.
АВ=20 см
АС- диагональ, АС=24см
Найти ВД.
Решение.
Обозначим точку пересечения диагоналей О.
Рассмотрим Δ АВО, он прямоугольный, т.т. диагонали ромба взаимно перпендикулярны.
ВО² = АВ² - АО² по теореме Пифагора
АО=1/2 АС, т.к. диагонали ромба в точке пересечения делятся пополам
АО= 24 : 2 = 12(см)
ВО²=20² - 12² = 256
ВО=√256 = 16 (см)
ВД= 2ВО=16*2=32(см)

Р= АВ+ВС+СД+АД
АВ²=АО²+ВО²=(24/2)²+(18/2)²=12²+9²=144+81=225
АВ=√225=15
АВ=15(см) сторона
18*12=216(см²) площадь ромба
216 : 15 = 14,4(см) расстояние между параллельными сторонами
Р= 15+15+15+15=60(см), т.к. все стороны ромба равны

4,6(76 оценок)

Ответ:

123123ilya

20.03.2022

РОмб АВСД, АВ=20, ВД=24, О точка пересечения диагоналей, диагонали в ромбе пересекаются под углом 90 и вточке пересечения делятся пополам, ВО=ОД=ВД/2=24/2=12, треугольник АОВ прямоугольный, АО=корень(АВ в квадрате-ВО в квадрате)=корень(400-144)=16, АС=2*АО=2*16=32 №2 ромб АВСД, АС=24, ВД=18, АО=ОС=24/2=12,. ВО=ОД =ВД/2=18/2=9, треугольник АВО прямоугольный, АВ=корень(АО в квадрате+ВО в квадрате)=корень(144+81)=15-сторона ромба, периметр АВСД=4*15=60 , площадь АВСД=1/2*АС*ВД=1/2*24*18=216 проводим высоту ВН на АД, ВН=площадь/АД=216/15=14,4-расстояние между параллельными сторонами

4,5(89 оценок)

Открыть все ответы

Ответ:

erra1337

20.03.2022

Треугольники AMC и BMC подобны. В подобных треугольниках углы попарно равны. ∠АМС=∠ВМС - по условию. ∠ВСМ≠∠АСМ в противном случае дуга АД была бы равной дуге АД, что в свою очередь ведет к равенству дуг СВД и САД. Из этого получим, что СД - диаметр окружности, перпендикулярный хорде. Тогда получим, что АМ=МВ, что противоречит условию задачи.
Значит ∠ВСМ=∠САМ. Составим отношение сходственных сторон в подобных треугольниках. АС/СВ=СМ/МВ=АМ/СМ. В два последних отношения подставим известные данные, получим СМ/9=4/СМ, СМ²=36, СМ=6
Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды. АМ*МВ=СМ*МВ

4*9=6*х, х=6
СД=СМ+МД=6+6=12(см)

4,5(56 оценок)

Ответ:

dlink162

20.03.2022

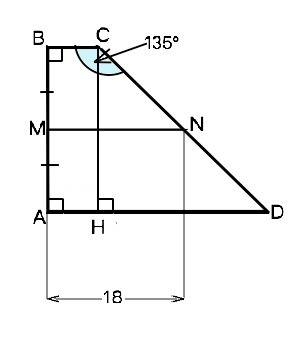
По условию АВ⊥АD, ВС║AD, значит, АВ⊥ВС ⇒ трапеция АВСD - прямоугольная. Средняя линия МN=(ВС+AD):2 ⇒ BC+AD=2•MN=2•18=36. BC:AD=1:8, следовательно, AD=8BC и сумма оснований равна BC+8BC=9BC ⇒ BC=36:9=4. AD=8•4=32.

Сумма углов при одной стороне трапеции равна 180° (внутренние односторонние). Поэтому угол СDA=45°. Опустим из вершины С высоту СН. AH=BC=4. Отрезок НD=32-4=28. Треугольник СНD прямоугольный. Из суммы углов треугольника ∠DСH=180°-90°-45°=45° ⇒ ∆ СDH - равнобедренный. СН=НD=28. По построению СН⊥AD и АВ⊥AD по условию. Два перпендикуляра между параллельными сторонами равны. ⇒ АВ=СН=28 (ед. длины)