1) Решим задачу используя уравнение пучка прямых y - y1 = k(x - x1).
Уравнение прямой, проходящей через две точки, находим по формуле:
(x–x1)/(x2–x1) = (y–y1)/(y2–y1)
уравнение прямой ВС: (x+1)/(5+1) = (y–1)/(4-1)
3(x+1) = 6(y–1)
x - 2y + 3 =0 уравнение высоты АЕ
Угловой коэффициент данной прямой k1 = ½
тогда угловой коэффициент прямой, ей перпендикулярной, k2 = -2
Подставив в уравнение пучка прямых k2, а вместо x1 и y1 координаты данной точки A(-3,-3), найдем y-(-3)=-2(x-(-3)), или y + 3 = -2x - 6, и окончательно 2x+y+9=0.
2) Так как точка K является серединой стороны AB, её координаты равны полусумме координат точек A и B:
K = (A+B)/2 = ((-3-1)/2; (-3+1)/2) = (-2; -1)
Подставляем значения:
(x-5)/(-2-5) = (y–4)/(-1–4)
(x-5)/7 = (y–4)/5
5(x-5) = 7(y–4)
5x - 25 = 7y – 28
5x –7y + 3 = 0 уравнение медианы СК
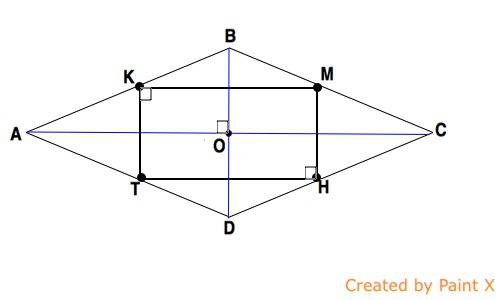
Докажите, что середины сторон ромба являются вершинами прямоугольника
Пусть дан ромб АВСD, точки К, М, Н и Т - середины его сторон. Соединим их последовательно.
Диагонали ромба АС и ВD пересекаются под прямым углом и каждая делит ромб на два равных треугольника, a АК=КВ, ВМ=МС, СН=НD и DТ=ТА по условию. ⇒
КМ и ТН - средние линии равных треугольников АВС и СDТ и параллельны диагонали АС ромба. ⇒ КМ=ТН
Аналогично ТК и МН - средние линии треугольников АВD и СВD и параллельны диагонали ВD ромба. ⇒ КТ=МН.
Стороны четырехугольника ТКМН параллельны и равны - КМНТ - параллелограмм.
Диагонали ромба точкой их пересечения делятся пополам и, пересекаясь, делят четырехугольник ТКМН на 4 равных параллелограмма, углы которых при точке пересечения диагоналей ромба О прямые. ⇒
Углы К, М, Н и Т противоположны углам при О и по свойству углов параллелограмма равны им. Следовательно,
четырехугольник ТКМН - прямоугольник с вершинами в серединах сторон ромба, что и требовалось доказать.