252 ед².
Объяснение:
В равностороннем треугольнике стороны равны, а все углы по 60°.
ВА = ВС = АС = 18:3 = 6 ед.
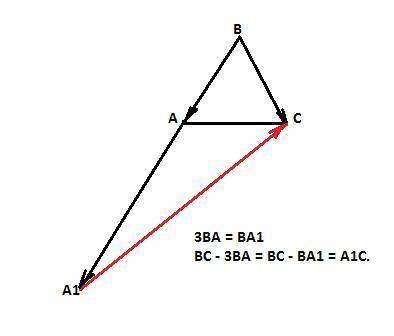
Вектор (ВС - 3ВА)² - это квадрат модуля вектора |ВС - 3ВА|.
Вектор 3ВА= ВА1 = 18 ед. (равен трем коллинеарным векторам ВА, расположенным на одной прямой, конец которого будет в точке А1).
По правилу вычитания векторов имеем:
ВС - 3ВА = ВС - ВА1 = А1С.
Вектор А1С² находим по теореме косинусов:
|A1С|² = |BC|² + |BA1|² - 2|BC|·|BA1|·Cos60 =>
|A1С|² = |6|² + |18|² - 2·6·18·(1/2) = 252 ед.
Но А1С² это как раз искомый вектор.
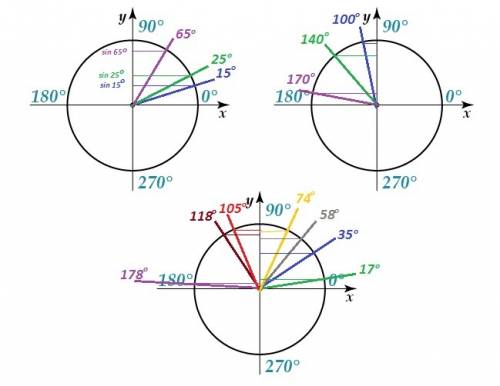
Можно воспользоваться правилом, что синус угла от 0° до 90° возрастает, синус угла от 90° до 180° убывает.
а) sin 15°; sin 25°; sin 65°
б) sin 170°; sin 140°; sin 100°
в) Использовать формулу приведения, чтобы свести все углы в первую четверть.
sin (180° - α) = sin α
sin 105° = sin (180° - 75°) = sin 75°
sin 118° = sin (180° - 62°) = sin 62°
sin 178° = sin (180° - 2°) = sin 2°
Синусы углов в первой четверти возрастают
sin 2°; sin 17°; sin 35°; sin 58°; sin 62°; sin 74°; sin 75°
Тогда синусы возрастают для углов
sin 178°; sin 17°; sin 35°; sin 58°; sin 118°; sin 74°; sin 105°
==========================================
Нарисовать углы на единичной окружности и отметить синусы на оси OY.
=>
треугольник равнобедренный и второй катет равен 12
площадь прямоугольного треугольника равна произведению катетов поделить на 2
S=12*12/2=72