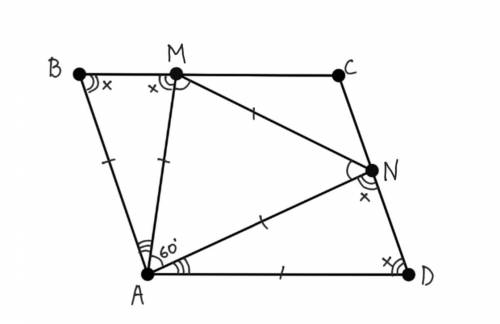
Дано: ABCD — ромб, М ∈ ВС, N ∈ CD, ΔAMN — равносторонний, MN=AD.
Найти: ∠АВС.
Решение.
1) У равностороннего треугольника все стороны равны.
Значит, AM=MN=AN. Известно, что MN=AD => AN=AD => ΔDAN равнобедренный, ∠ADC=∠AND=x.
2) У ромба все стороны равны и противоположные углы равны.
∠АВС=∠ADC=x. То есть значение "х" и будет нашим ответом.
AB=AD=AN, AN=AM => AB=AM, ∠ABM=∠AMB=x.
3) У равностороннего треугольника все углы равны по 60°. Значит, ∠AMN=∠MNA=∠NAM=60°.
4) Сумма углов, прилежащих к одной стороне ромба, равна 180°. Отсюда, ∠ADC+∠BAD=180°.
∠BAD= 180°–∠ADC= 180°–x.
5) Сумма углов каждого треугольника равна 180°. А это означает, что в ΔBAM ∠BAM= 180°–2x,
в ΔDAN ∠DAN=180°–2x,
откуда следует, что
∠BAM=∠DAN=180°–2x.
6) С пунктов 4 и 5 можем выразить угол BAD и таким образом найти значение "х".
∠BAD=180°–x.
∠BAD=∠BAM+∠DAN+∠NAM= 2(180°–2x)+60°.
Приравняем:
180°–х=2(180°–2х)+60°;
180°–х=360°–4х+60°;
–х+4х=360°+60°–180°;
3х=240°;
х= 80°.
х=∠АВС=80°.
ОТВЕТ: 80°.
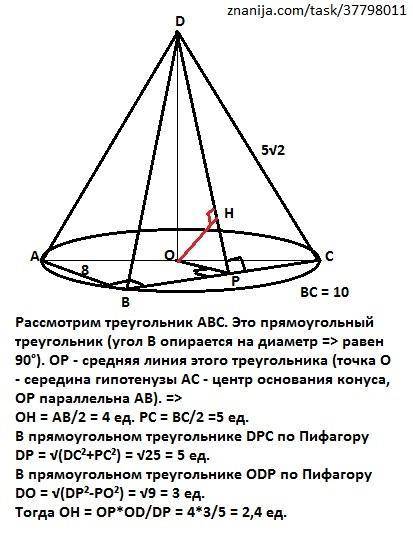
Искомое расстояние равно 2,4 ед.
Объяснение:
Расстояние от точки О до плоскости DCB - это перпендикуляр ОН, опущенный из этой точки на плоскость.
Проведем перпендикуляр ОР из точки О к прямой ВС.
По теореме о трех перпендикулярах DР перпендикулярна ВС.
Тогда в прямоугольном треугольнике OРD (DO перпендикулярна плоскости основания конуса - дано) высота ОН из прямого угла и есть искомое расстояние.
Рассмотрим треугольник АВС. Это прямоугольный треугольник (угол В опирается на диаметр => равен 90°). ОР - средняя линия этого треугольника (точка О - середина гипотенузы АС - центр основания конуса, ОР параллельна АВ). =>
OH = AB/2 = 4 ед. РС = ВС/2 =5 ед.
В прямоугольном треугольнике DРС по Пифагору
DP = √(DC²+PС²) = √25 = 5 ед.
В прямоугольном треугольнике ОDР по Пифагору
DО = √(DР²-PО²) = √9 = 3 ед.
Тогда ОН = OP*OD/DP = 4*3/5 = 2,4 ед.
а) АД
б) в треугольнике А1АВ надо провести высоту АН - это и будет расстояние
в) ВА
г) в треугольнике АВС надо провести высоту ВН - это и будет расстояние