Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
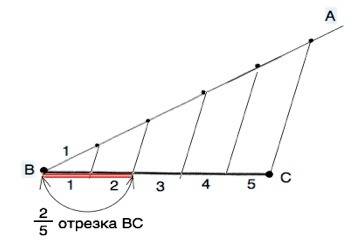
Пусть дан отрезок ВС.
От конца В отрезка начертить луч и на нем от В отметить через равные промежутки 5 точек. Из пятой точки провести прямую через т.С отрезка ВС и провести параллельно ей прямые, пересекающие отрезок ВС. Этими прямыми ВС будет разделен на 5 равных частей. Любые две соседние части равны 2/5 исходного отрезка ВС.
есть формула 1 + tg^2(x) = 1/cos^2(x)
из нее 1 + 9/16 = 1/cos^2(x)
cos^2(x) = 16/25
cos(x) = +- 4/5 (так как не задан промежуток угла альфа, то два ответа)
из формулы sin(x)/cos(x) = tg(x) найдем sin:
sin(x) = tg(x)*cos(x)
sin(x)1 = 3/4*4/5= 3/5
sin(x)2 = 3/4*(-4/5)= -3/5