Площадь боковой поверхности усеченного конуса находят по формуле:
S=π(r₁+r₂)l, где r₁ и r₂ радиусы оснований, а l - образующая.
Образующую предстоит найти.
Представим осевое сечения этого усеченного конуса.
Это - равнобедренная трапеция, основаниями которой являются диаметры оснований конуса, боковыми сторонами - образующая.
Известно, что высота, опущенная из вершины тупого угла на большее основание, делит его на отрезки, меньший из которых равн полуразности оснований.
Опустим эту высоту и получим прямоугольный треугольник с катетами:
1) полуразность оснований и
2) высота трапеции,
гипотенузой будет боковой сторона, и острый угол между большим основанием и боковой стороной равен 30 градусам.
Полуразность оснований =( 2r₁-2r₂):2=4
Косинус угла 30 градусов равен (√3):2
Образующая = 4:сos 30=8:√3
S=π(14+18)*8:√3=256π:√3= ≈ 464,346
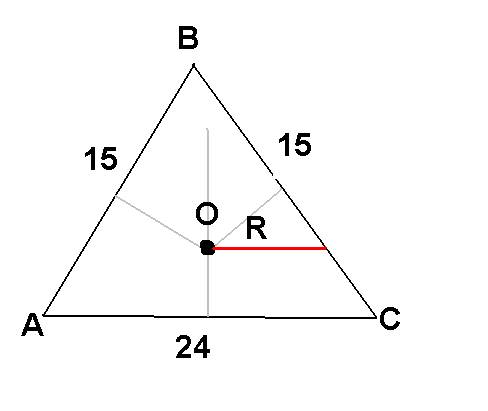
1) треугольки АBC - равнобедренный, AB=15 см, ВС=15 см, АС=24 см, треугольник АВС - вписанный в окружность, О- описанная окружность около треугольника АВС.
2) Формула радиуса описанной окружности:
R= abc / 4S ;
2) По формуле герона S= арифметический квдратный корень из p(p-a)(p-b)(p-c);
Найдем полупериметр,
p= P/2= (a+b+c)/2 = (15+15+24)/2 = 54/2 = 27.
3) Подставим числовые значения в формулу
S= арифметический квадратный корень из 27(27-15)(27-15)(27-24) = арифметический квадратный корень из 27*12*12*3= арифметический квадратный корень из 11664 =
108 (см квадратных).
4) Найдем Радиус описанной окружности (подставим числовые значения в формулу из 2 действия):
R= (15*15*15 )/ 4*108 = 5400 / 432 = 12,5 cм.
ответи: 12,5 см.
Из треугольника АВС по теореме косинусов найдем косинус угла В:
AC² = AB² + BC² - 2·AB·BC·cosB
cosB = (AB² + BC² - AC²) / (2·AB·BC)
cosB = (40² + 40² - 20²) / (2 · 40 · 40) = 7/8
ВН : НС = 3 : 1, значит НС = 1/4 ВС = 1/4 · 40 = 10 см
ВН = 40 - 10 = 30 см
Из треугольника АВН по теореме косинусов найдем АН:
АН² = AB² + BH² - 2·AB·BH·cosB = 40² + 30² - 2 · 40 · 30 · 7/8
AH² = 1600 + 900 - 2100 = 2500 - 2100 = 400
AH = 20 см