Объяснение:
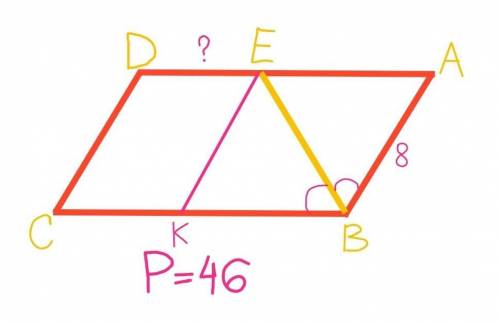
Из точки Е проведем отрезок ЕК, параллельный АВ.
Противоположные стороны параллелограмма параллельны, тоесть СВ//DE => ЕА//КВ и DE//CK
Так как в четырехугольнике КЕАВ стороны попарно параллельны, следовательно КЕАВ – параллелограмм.
ВЕ – биссектриса угла КВА по условию и диагональ параллелограмма КЕАВ.
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб.
Следовательно: КЕАВ – ромб
У ромба все стороны равны. Исходя из этого: ЕА=КВ=АВ=8 см.
СD=AB=8 так как противоположные стороны параллелограмма равны.
Р(АВСD)=АВ+ВС+CD+AD=AB+BK+KC+CD+DE+EA=8+8+KC+8+DE+8=32+KC+DE
Так как Р(ABCD)=46 см по условию, то получим уравнение:
32+КС+DE=46
KC+DE=14 см
Так как ЕК//АВ, а АВ//CD, то ЕК//CD;
DE//CK (доказано ранее);
Исходя из этого: CDEK – параллелограмм.
Противоположные стороны параллелограмма равны, тоесть DE=CK.
Тогда 2DE=14 см
DE=7 см
ответ: 7 см
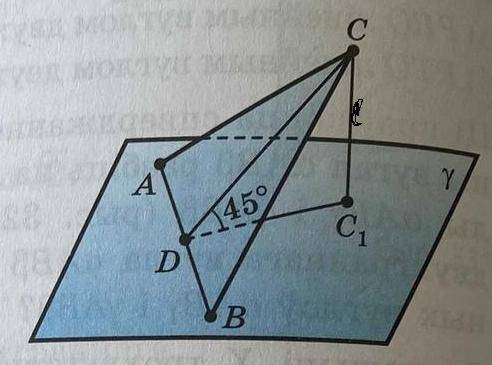
@ 319. через гипотенузу АВ равнобедренного прямоугольного треугольника- ка АВС под углом в 45° к его плоскости проведена плоскость расстояния от вершины прямого угла С на (рис. 326). Найдите площадь треугольника АВС[email protected]
Объяснение:
Т.к. проведена " плоскость на расстояния от вершины прямого угла С ", то СС₁⊥ γ ⇒Δ СС₁D-прямоугольный , sin45°=СС₁/DC ,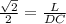 
,DС=L√2.
Т.к.ΔАВС-равнобедренный, прямоугольный , то ∠А=∠В=45°⇒ΔACD-равнобедренный ⇒AD=DС=L√2.
И ΔВCD-равнобедренный ⇒ВD=DС=L√2.
Значит АВ=2L√2.
S=1/2*a*h , S(АВС)=1/2*2L√2*L√2=2L² .
