Высота в прямоугольном треугольнике равна среднему пропорциональному проэкций катетов на гипотенузу. (h = корень с а(с) * b(c) ). Также катет прям треуг равен сред пропорц гипотенузы и его проэкции на гипотенузу, значит проэкция катета равна квадрату катета, разделённого на гипотенузу. (а(с) = а^2/с; b(c) = b^2/c). Квадрат гипотенузы, по теореме Пифагора, равен суме квадратов катетов (9+36=45). Гипотенуза равна трём кореням с пяти. а(с)=9/3 кор с 5 = 3/кс5; b(c)= 36/3кс5= 12/кс5. Следовательно, h^2= 3/кс5 * 12/кс5 = 36/5 = 7,2; h = корень с 7,2 = 2,7.
Что-то не так. Во-первых, опечатка - не призма, а пирамида. Во-вторых, она должна быть 4-угольной, потому что 4 угла куба не могут лежать на трех апофемах треугольной пирамиды. Значит, считаем, что это 4-угольная правильная пирамида. В основании квадрат. В пирамиду вписан куб так, что 4 нижних вершины лежат на основании, а 4 верхних на апофемах (высоты боковых граней). Я сделал рисунок. Там много линий, и чтобы разобраться, я нарисовал апофемы красным, куб синим, а высоту пирамиды жирным черным. Нижние вершины куба лежат на средних линиях основания KM и LN. Справа я нарисовал сечение пирамиды плоскостью SLN. В сечении будет равнобедренный треугольник, а в него вписан прямоугольник PRR1P1, у которого высота PP1 = RR1 = x - стороне куба, а основание PR = P1R1 = x√2 - диагонали грани куба. Теперь решаем задачу. Сторона основания пирамиды а, диагональ AC = BD = a√2, OC = a√2/2, угол наклона бокового ребра α. В треугольнике AOS катет OS=H=AO*tg α=a*√2/2*tg α. В треугольнике LOS катет OL = a/2, по теореме Пифагора SL^2 = OL^2 + OS^2 = a^2/4 + a^2/2*tg α = a^2/4*(1 + 2tg α) SL = a/2*√(1 + 2tg α) Угол наклона апофемы к плоскости основания OLS = β: tg β = OS/OL = (a*√2/2*tg α) : (a/2) = √2*tg α В треугольнике RR1L катет RL = RR1/tg β = x/(√2*tg α) = x√2/(2tg α) Но мы знаем, что PR = x√2 и NP = RL. Получаем NL = NP + PR + RL a = 2*x√2/(2tg α) + x√2 = x√2/tg α + x√2
a=16 см - основание, b=c - боковые стороны, H=4см - высота;
R опис = abc/4S;
b=c=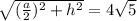 (см)
(см)
R опис =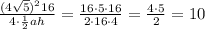 (см)
(см)