ответ: 337,5 см²
Объяснение:
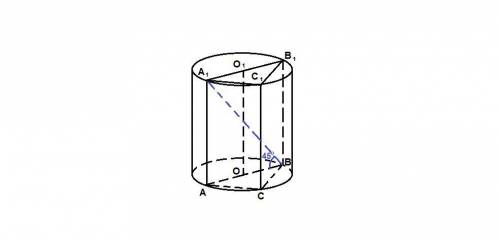
Так как цилиндр описан вокруг призмы, то основания призмы вписаны в основания цилиндра, боковое ребро призмы является высотой цилиндра.
Площадь полной поверхности цилиндра - это сумма площади боковой поверхности и площади двух оснований:
Sпов = 2πRh + 2 · πR²
Центр окружности, описанной около прямоугольного треугольника лежит на середине гипотенузы. Значит, радиус основания цилиндра равен половине гипотенузы:
ΔАВС: ∠С = 90°, по теореме Пифагора:
АВ = √(АС² + ВС²) = √(9² + 12²) = √(81 + 144) = √225 = 15 см
R = 1/2 AB = 7,5 см
Большая грань призмы - грань, содержащая гипотенузу основания.
Так как диагональ прямоугольника АВВ₁А₁ делит прямой угол пополам, то АВВ₁А₁ - квадрат. Тогда
h = AA₁ = AB = 15 см
Sпов = 2πRh + 2 · πR² = 2π · 7,5 · 15 + 2π · 7,5² =
= 225π + 112,5π = 337,5π см²
Внимание : тут два варианта .
96 или 78 см
Объяснение:
Вариант 1 (если бисс АК)
1) уг 1=уг 2 (как накрест лежащие при парал прямых);
уг 1=уг 3 (тк бисс);
тогда уг 2=уг3 => треуг АВК–равнобед =>АВ=ВК=19 и =СD (как стороны парал);
2) ВС=19+10=29=АD;
3) Р =( 19+29)*2=96 см
Вариант 2 (если бисс DК)
1) уг 1=уг 2 (как накрест лежащие при парал прямых);
уг 1=уг 3 (тк бисс);
тогда уг 2=уг3 => треуг DСК–равнобед =>DС=СК=10 и =АВ (как стороны парал);
2) ВС=19+10=29=АD;
3) Р =( 10+29)*2=78см
Чертёж в приложении.
Если что-то непонятно , пишите в комментах.
Успехов в учёбе! justDavid
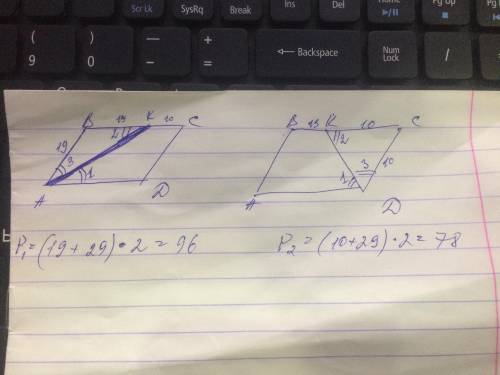
ВD=√(ВС^2+CD^2) = √(5^2+5^2)= √50= 5√2
BO= (5√2)/2
SD= √(6^2+((5√2)/2)^2)= √48,5
SK=√ ((√48,5)^2 - 2,5^2) =46