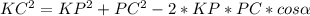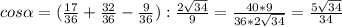Каждое ребро правильной шестиугольной призмы равно а. Найдите площадь поверхности призмы.
---
Призма называется правильной, если ее боковые ребра перпендикулярны основаниям, а основания – правильные многоугольники.
Все ребра правильной призмы равны, ⇒
каждая из 6 боковых граней – квадрат, площадь которого S=a².
Ѕ(бок)=6а²
Основания правильной шестиугольной призмы - правильные шестиугольники, состоящие из 6 равных правильных треугольников.
Формула площади правильного треугольника S=(a²√3):4 ⇒
Ѕ (осн)•2=2•6•(a²√3):4=3а²√3
Площадь поверхности призмы равна сумме площадей: площади боковой поверхности и двух оснований.
S (призмы)= 6а²*+3•a²√3 или 3а²•(2+√3) ≈11,2а²
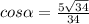
Объяснение:
Дано: Окр.OR-описанная
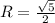
ΔАВС - прямоугольный
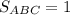
ВК и СМ - медианы
Найти: cosα
1. Окр. OR - описана около ΔАВС ⇒СВ - диаметр (прямой угол опирается на диаметр)
2. Рассмотрим ΔАВС - прямоугольный.
Пусть меньший катет = a, больший - b.
Тогда:
Площадь треугольника:
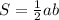
По теореме Пифагора:
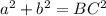
Составим систему:
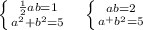
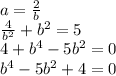
По теореме Виета:
Или
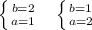
Тогда АС=1; АВ=2.
3. Рассмотрим ΔАВК - прямоугольный.
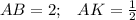(ВК-медиана)
По т. Пифагора
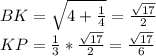(св-во пересекающихся медиан)
4. Рассмотрим Δ МАС - прямоугольный.
(СМ-медиана)
По т. Пифагора
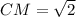
(св-во пересекающихся медиан)
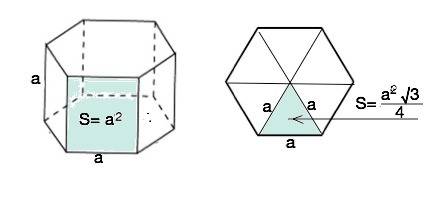
5. Рассмотрим ΔКРС
Используем теорему косинусов:
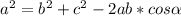
Имеем
