Правильная треугольная пирамида.
Сторона основания = 9
Боковое ребро = 6
Найти:S полн поверхности - ?
Решение:Обозначим данную пирамиду буквами ABCS.
AC = 9
SC = 6
Так как данная пирамида - правильная, треугольная => основание этой пирамиды - равносторонний треугольник.
Равносторонни треугольник - треугольник, у которого все углы и стороны равны.
=> АВ = ВС = АС = 9
S равностороннего △ = а²√3/4, где а - сторона Δ ABC.
S равностороннего △ = 9²√3/4 = 81√3/4 ед.кв.
S боковой поверхности = 1/2(Р осн * L), где Р - периметр основания; L - апофема.
Апофема - высота боковой грани правильной пирамиды, проведённая из её вершины.
SR - апофема
P (периметр) = (АВ + ВС + АС)/2 = (9 * 3) = 27
Апофема делит сторону основания на 2 равные части.
Так как ВС = 9 => BR = RC = 9/2 = 4,5
△SRC - прямоугольный, так как SR - высота.
Найдём апофему SR, по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты)
SR = √(SC² - RC²) = √(6² - (4,5)²) = 3√7/2
S боковой поверхности = (27 * 3√7/2)/2 = 81√7/4 ед.кв.
S полной поверхности = S основания + S боковой поверхности = 81√3/4 + 81√7/4 = 81/4 * (√3 + √7) = 20,25 * (√3 + √7) ед.кв.
ответ: 20,25 * (√3 + √7) ед.кв.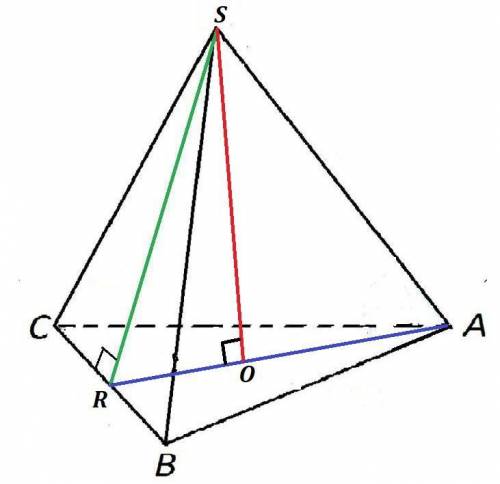
sinA=CD/AC
S=AD*CD
AD=cosA*AC=cos42*3=0,7431*3=2,2294
CD=sin42*3=0,6691*3=2,0074
S=2,2294*2,0074=4,4753 см²