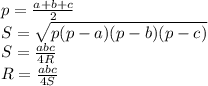

Sabcd = 30 кв. ед.
Объяснение:
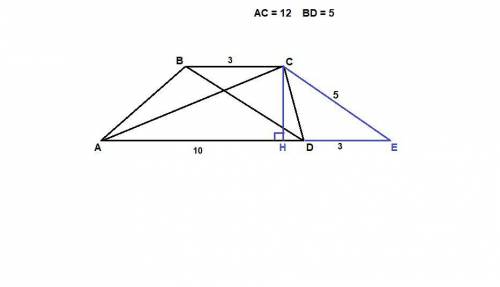
Проведем СЕ ║ BD, тогда BCED - параллелограмм, так его противоположные стороны параллельны. Значит,
СЕ = BD = 5
DE = BC = 3
Пусть СН - высота трапеции, тогда СН - и высота треугольника АСЕ.
Площадь трапеции:
Sabcd = 1/2 · (AD + BC) · CH
Площадь треугольника АСЕ:
Sace = 1/2 · AE · CH = 1/2 · (AD + DE) · CH = 1/2 (AD + BC) · CH = Sabcd
Итак, можно найти площадь треугольника АСЕ (в нем известны все три стороны). А площадь трапеции равна площади этого треугольника.
По теореме, обратной теореме Пифагора, проверим, не является ли этот треугольник прямоугольным:
AE² = AC² + CE²
13² = 12² + 5²
169 = 144 + 25
169 = 169 - равенство верно, треугольник прямоугольный.
Sace = 1/2 · AC · CE = 1/2 · 12 · 5 = 30
Sabcd = 30 кв. ед.
Угол В = 75 ° , угол С = 90 °
Сумма углов треугольника = 180 °
Угол А + угол В + угол С = 180 °
Угол А = 15 °
Угол С (90°) - наиб. => сторона АВ - наибольшая
Угол А (15°) - наим. => сторона ВС - наименьшая