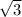Задача:
Длина окружности, вписанной в правильный треугольник, равна 12π см. Найдите периметр треугольника.
Чтобы найти периметр правильного Δ, нужно знать сторону; что найти сторону, нужно найти радиус вписанной окружности.
Дня нахождения радиуса окружности, воспользуемся формулой длины окружности и выразим из нее радиус:
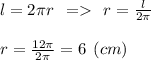
Теперь воспользуемся формулой радиуса вписанной окружности в правильный треугольник для нахождения стороны Δ:
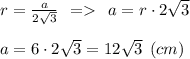
Осталось за малым — периметр правильного треугольника:
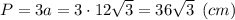
Периметр треугольника равен 36√3 см.
Угол MAD=30 градусов (90-30-30=30). Треугольник MAD прямоугольный (прямой угол D). Т.к. AKCM - ромб, все его стороны равны (AK=KC=CM=AM). Решим через косинус. Косинус - это отношение прилежащего катета к гипотенузе. Итак, косинус 30 градусов=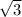 \2=3\AM.
\2=3\AM.
Поэтому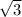 AM=6
AM=6
AM=2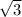
AM=KA=2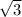
ответ: 2