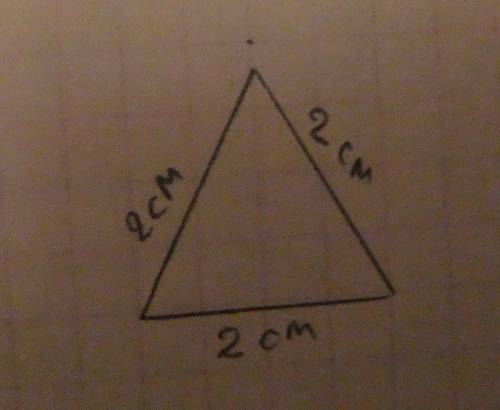
1) Чертим произвольную прямую. Отметим на ней т.О. Ставим остриё циркуля в т.О и по обе её стороны отмечаем на прямой т.1 и т.2.
2) Из т.1 и т.2 как из центра раствором циркуля, большим чем расстояние от них до т.О, чертим две полуокружности. Точки их пересечения соединяем. Построег прямой угол. ( это стандартный деления отнезка - в данном случае отрезка 1-2- пополам и возведения перпендикуляра)
3) Из т. О, как из центра, проводим окружность. Точки ее пересечения со сторонами прямоуго угла А и В.
Содединим А и В. Треугольник АОВ - прямоугольный равнобедренный -АО=ВО.
4 ) Делим отрезок АВ пополам ( см. п.2).
ОС - высота. медиана и биссектриса треугольника АОВ. Угол АОВ=СОВ=45°
5) Ставим ножку циркуля в т.С и тем же радиусом, что проведенная окружность, отмечаем на ней точку D. ∆ СОD- равносторонний, угол СОD=60°
Угол АОD=60°-45°=15°.
Нужные углы построены.
Расстояние от вершины А до точки пересечения медиан равно 8см.
Объяснение:
Медианы, пересекаясь, делятся точкой пересечения в отношении 2:1, считая от вершины.
В равнобедренном треугольнике медиана, проведенная к основанию, является и высотой. Проведем медиану AD к основанию ВС. Тогда BD=DC = BC:2 = 5см.
В прямоугольном треугольнике АВD по Пифагору катет
BD = √(АВ² - BD²) = √(13² - 5²) =12см.
Точка пересечения О делит медиану BD в отношении
АО/ОD = 2/1, считая от вершины А (свойство медиан). Значит расстояние от точки А до точки О равно 12·2/3 = 8 см.