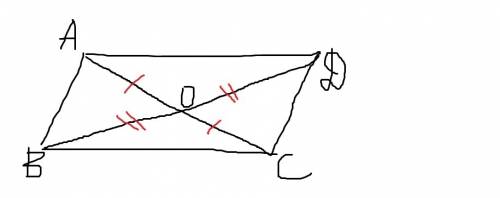
Рассмотрим треугольники AOD и COB.
AO=OC
BO=OD
∠AOD=∠COB (вертикальные)
Значит, треугольники AOD и COB равны (по двум сторонам и углу между ними).
∠ADO=∠CBO (если треугольники равны, то и соответствующие углы тоже равны). Эти углы — внутренние накрест лежащие при прямых AD и BC и секущей BD.
AD∥BC (по признаку параллельных прямых)
AOB=COD, ∠ABO=∠CDO и AB∥CD (аналогично треугольникам AOD и COB.
Доказали, что AD∥BC и AB∥CD
Значит, ABCD — параллелограмм (по определению)
ОМ перпендикулярен МК.
ON перпендикулярен КN.
Отрезки касательных проведённых из общей точки равны, а луч проведённый из общей точки через центр окружности является биссектрисой угла.
Угол МКО=углу NKО=60.
Угол МОК=углу NOK=90-60=30
Против угла в 30 градусов в прямоугольном треугольнике лежит катет равный половине гипотенузы.
МК=NK=12/2=6
ответ: МК=NK=6.