P=12
Объяснение:
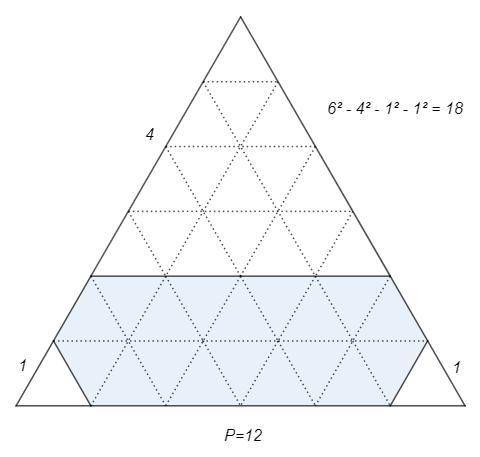
Поскольку стороны искомого шестиугольника целочисленные, а углы 120, будем решать на сетке из единичных равносторонних треугольников (ед.).
Правильный шестиугольник со стороной 1 состоит из 6 ед., искомый шестиугольник - из 18 ед.
Искомый шестиугольник виден, его периметр 12.
Попробуем доказать перебором, что он единственный.
Любой шестиугольник с углами 120 (внешние углы 60) можно достроить до равностороннего треугольника, продлив стороны.
Количество ед., из которых состоит равносторонний треугольник, равно квадрату его стороны (сумма последовательных нечетных чисел равна квадрату).
От равностороннего треугольника со стороной t нужно отсечь равносторонние треугольники со сторонами a, b, c и получить площадь 18 ед.
t^2 -a^2 -b^2 -c^2 =18
Из рисунка видно, что t не может быть больше 6 (фигура высотой 1 ед. будет параллелограммом или трапецией, но не шестиугольником).
Перебирая квадраты целых чисел, находим единственное решение:
6^2 -4^2 -1^2 -1^2 =18
2) Находим уравнение плоскости α, проходящей через точку Р1(−4, 3, 5) и перпендикулярной заданной прямой L = Р1Р2:
(x + 4)/1 = (y − 3)/4 = (z − 5)/(−1).
Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n={A, B, C} представляется формулой:
A(x−x0)+B(y−y0)+C(z−z0) = 0. (2)
Направляющий вектор прямой L имеет следующий вид:
q = {m, p, l} = {1, 4, −1} (3)
Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (2) примет следующий вид:
m(x−x0)+p(y−y0)+l(z−z0) = 0 (4)
Подставляя координаты точки Р1 и направляющего вектора q в (4), получим:
1(x−(−4))+4(y−3)−1(z−5) = 0 (5)
Упростим уравнение (5): x+4 y−1 z−3 = 0. (6)
ответ. Уравнение плоскости, проходящей через точку Р1(−4, 3, 5) и перпендикулярной прямой (1) имеет вид x+4 y−1 z−3 = 0.
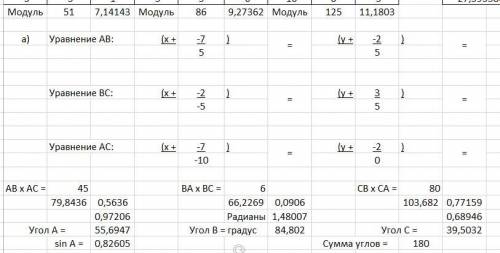
3) Дан треугольник ABC с вершинами A(7;2;3), B(2;-3;4), C(-3;2;-2).
Точка А Точка В Точка С
x y z x y z x y z
7 2 3 2 -3 4 -3 2 -2
Вектор АВ Вектор ВС Вектор АС
x y z x y z x y z
-5 -5 1 -5 5 -6 -10 0 -5
Модуль 51 7,14143 Модуль 86 9,27362 Модуль 125 11,18034
АВ х АС = 45 ВА х ВС = 6 СВ х СА = 80
79,8436 0,5636 66,22688 0,090598 103,6822 0,771588515
0,972056618 Радианы 1,480074279 0,689461756
Угол А = 55,69474166 Угол В = градус 84,80200957 Угол С = 39,50324876.
Данные расчёта в программе Excel плохо форматируются, поэтому дано фото во вложении.
третья сторона длжна быть больше 12м(лежит против большего угла, значит должна ыть большей стороной) но меньше 18( т.к. сторона треугольника должна быть меньше суммы двух других)
сделовательно, учитывая то, что ее длина должна быть целым числом, это 14 или 16 метров
вроде так, но тут я не увернена