В прямокутному трикутнику катет довжиною 15 см прилягає к куту 30°. Знайдіть бісектрису другого гострого кута цього трикутника.
В прямоугольном треугольнике катет длиной 15 см прилегает к углу 30 °. Найдите биссектрису второго острого угла этого треугольника.
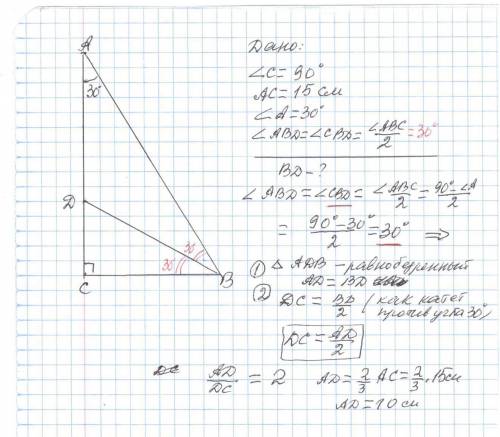
Дано :
∠C =90° ;
AC =15 см ;
∠A =30 ° ;
∠ABD =∠CBD = ∠ABC /2 ( BD _биссектриса )
-----------------
BD - ?
∠ABC = 90° - ∠ A =90° -30° =60°
∠ABD =∠CBD = ∠ABC /2 = 60°/2 = 30° , следовательно
1. ΔADB равнобедренный AD = BD и
2. из ΔDBC: CD = BD /2 как катет против угла ∠CBD =30°
CD / AD = 1/2 ⇔ 1 +CD / AD = 1/2 +1 ⇔AC/AD =3/2 ⇒AD =(2/3)*AC
AD =2*15 см / 3 = 10 см
ответ : BD= AD = 10 см .
- - - - - - - - - -
2-ой
CD /AD = BC / BA ( теорема о биссектрисе )
CD /AD =1/2 BC = BA/2 (снова как катет против угла A =30°)
* * * * * * * рисунок во приложении * * * * * * *
Объяснение:
5. Треугольники равны по двум сторонам и углу между ними (<BAD = <CDA, AD -общая сторона, AC=BD)
6. т О - точка пересечения высот
Тр-к AMC - прямоугольный. <MAC = 90 - 40 = 50
Тр-к ANC - прямоугольный. <NCA = 90 - 80 = 10
Тр-к AOC: искомый угол <AOC = 180 - (50+10) = 120
7. Тр-к CBD - прямоугольный и р/б, т.к. углы при основании равны 45
DB = CB = 10. По т. Пифагора BC = √(2DB^2) = 10√2
Тр-к ABC - прямоугольный и р/б, т.к. углы при основании равны 45
BC = AC. По т. Пифагора AB = √(2BC^2) = 20 см