Решение
Объяснение:
Радиус вписанной в равнобедренную трапецию окружности равен половине ее высоты.
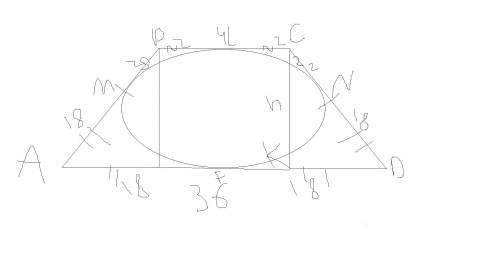
Назовем трапецию ABCD (BC ║ AB), проведем высоту CK к точке K.
Вписанная окружность прикасается к серединам сторон.
Обозначим эти середины: M (AB), L (BC), N (CD), F (AD).
Касательные, проведенные с одной точки равны:
BM = BL = CL = CN = 2
AM = AF = DF = DN = 18
CD = 2 + 18 = 20
Рассмотрим ΔCKD:
∠CKD = 90° (CK - высота)
KD = (AD - BC) / 2 = (36 - 4) / 2 = 32/2 = 16 (по свойству равнобедренной трапеции)
KD = 16
По теореме Пифагора:
CK² = CD² - KD²
CK = √(400 - 256) = √144 = 12
CK = 12
r = CK/2 = 12/2 = 6
r = 6 см
Синус острого угла прямоугольного треугольника- отношение противолежащего катета к гипотенузе, косинус -отношение прилежащего катета к гипотенузе, тангенс - отношение противолежащего к прилежащему катету.
Когда нет возможности воспользоваться тем, что треугольник прямоугольный еще и равнобедренный, или свойством угла в 30 градусов, чтобы найти прилежащий, противолежащий катеты или гипотенузу, используют синус, косинус и тангенс острого угла. Например, при нахождении прилежащего к углу в 60° катета, если есть гипотненуза в 4см, этот катет равен 4*0,5=2/см/, т.к. катет равен гипотенузе, умноженной на косинус угла в 60°.
Например, при решении стереометрических задач, где потребуется нахождение элементов пирамиды, призмы, конуса, тоже будет использоваться этот материал. Поэтому его надо досконально знать, а значения таблицы для 30°, 45°, 60° запомнить.