Задача решена Пользователем Рисадес Хорошист
Исправлена неточность в последнем действии.
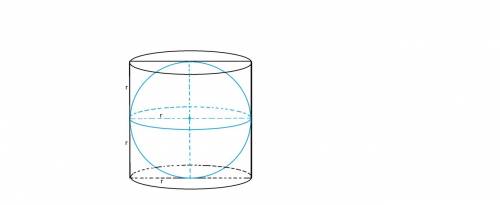
Шар может быть вписан в цилиндр только тогда, когда этот цилиндр правильный, т.е. когда его осевое сечение является квадратом.
Радиус основания цилиндра равен радиусу шара и равен r.
Высота цилиндра равна диаметру основания и равна 2 r.
Полная площадь поверхности складывается из площади двух оснований и площади боковой поверхности:
2*πr² + 2πr*2r = 6πr²
Площадь шара = 4πr²
Площадь цилиндра больше площади шара в
6πr² : 4πr² = 1,5 (раза)
Площадь полной поверхности шара
111 : 1,5 = 74 ( единиц площади)
а где продолжение условия? основанием пирамиды dabc является правильный треугольник abc сторона которого = ребро da перпендикулярно к плоскости авс , а плоскость dbc составляет с плоскостью авс угол 30*. найдите площадь боковой поверхности пирамиды. условие такое? если такое, то вот решение : s(бок) = 2s(адс) + s(всд) угол дка = 30, тогда ад = ак* tg30 = (av3/2)*v3/3 =a/2 тогда s(асд) = 1/2*а*а/2 = а^2 / 4 дк = а, тогда s(всд) = 1/2*а*а = а^2 / 2 s(бок) = 2*(а^2 / 4) * (а^2 / 2) = а^2
По т.Пифагора найдем АС:
АВ²=АС²+ВС²
АС²=АВ²-ВС²
АС²=120-24
АС=4√6.
tgА= ВС/АС
tgА= 2√6/4√6=0,5
ответ : tgA=0,5