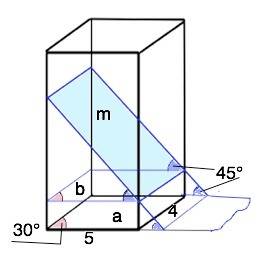
Пусть плоскость m - искомая.
Тогда плоскость а основания является её ортогональной проекцией на плоскость, содержащую основание призмы.
Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекции.
S (a)=S(m)•cos45°⇒
S(m)=S(a):cos45°
Формула площади параллелограмма
S=a•b•sinα, где а и b стороны параллелограмма, α - угол между ними.
S(a)=4•5•sin30°=20•1/2=10 дм²
cos45°=√2/2 или иначе 1/√2
S(m)=10:(1/√2)=10√2 см²
AB=8, BC=15, AC=17
AC^2=AB^2+BC^2
Значит, треугольник ABC - прямоугольный
S=пR^2
R=AC/2=8.5
S=3.14*8.5^2=226.865