Обозначим :
Н - высота пирамиды
h - высота основания пирамиды
r -радиус окружности, вписанной в основание
а - сторона основания
Решение
а) высота пирамиды Н = L· sinβ
б) проекция апофемы на плоскость основания -это радиус вписанной окружности r = L · cosβ.
в) сторона основания пирамиды а = 2r/tg 30° = 2L· cosβ/(1/√3) =
= 2√3 · L·cosβ
г) площадь основания пирамиды Sосн = 0.5h·a, где h = a·cos30°.
Тогда Sосн = 0.25a²·√3 = 0.25 · √3 · (2√3 · L·cosβ)² = 3√3L² · cos²β
д) Площадь боковой поверхности пирамиды
Sбок = 3 · 0,5 · L · a = 1.5L · 2√3 · L·cosβ = 3√3 · L² · cosβ
e) площадь полной поверхности пирамиды:
Sполн = Sосн + Sбок = 3√3 · L² · cos²β + 3√3 · L² · cosβ =
= 3√3 · L² · cosβ · (cosβ + 1)
Подробнее - на -
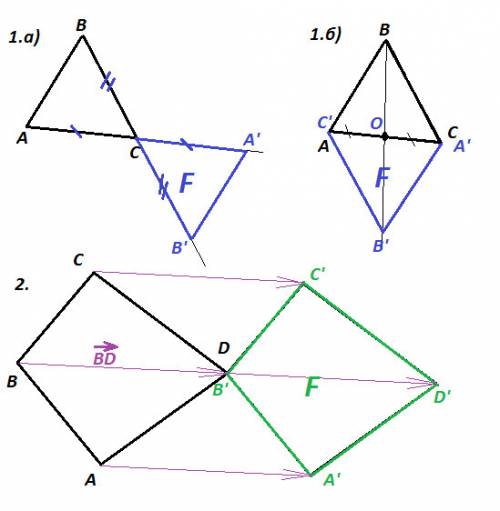
1. а) Продлить отрезок АС за точку С. Отложить от точки С отрезок СА', равный отрезку AC. Продлить отрезок BС за точку С. Отложить от точки С отрезок СB', равный отрезку BC. Соединить точки A' B'. Полученный треугольник A'B'C симметричен исходному треугольнику ABC относительно точки С - точка С осталась на месте как центр симметрии.
1.б) Отметить середину отрезка AC - точку О. AO = OC ⇒ A'=C; C'=A. Провести прямую через точки B и О, отложить от точки О отрезок OB', равный отрезку OB. Полученный треугольник AB'C симметричен исходному треугольнику ABC относительно точки О - середины отрезка АС.
2. Поправка к условию. Так как у треугольника 3 вершины, то фигура АВСД не может быть треугольником. Дан четырёхугольник АВСД. Через каждую вершину нужно провести прямую, параллельную вектору BД, по этим прямым в одном направлении отложить отрезки, равные отрезку BД. Точка В' совпадёт с точкой Д. Полученная фигура А'ДС'Д' равна исходной фигуре АВСД.
Нет. В параллелограмме диагонали точкой пересечения делятся пополам. АС=20, АО=10, диагональ точкой пересечения делится пополам. ВD=15, ВО=7, диагональ точкой пересечение не делится пополам.