75 (единиц)
Объяснение:
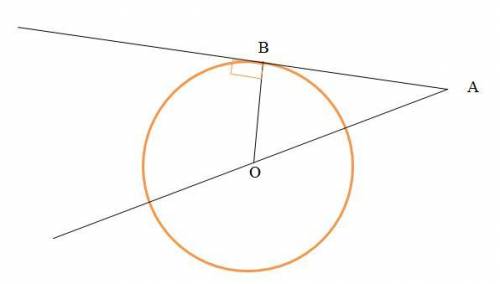
Дано (см. рисунок):
Окружность с центром в точке О
Касательная АВ и длина отрезка АВ=40 (ед.)
Секущая АО и длина отрезка АО=85
Найти: R=OB.
Решение.
Один из свойств касательной:
Касательная АВ к окружности с центром в точке О перпендикулярна радиусу R, проведенному в точку касания В.
В силу этого треугольник AOB прямоугольный и:
∠B=90°, AO – гипотенуза, AB и OB катеты.
Для прямоугольного треугольника AOB верна теорема Пифагора:
AO² = OB² + AB².
Отсюда
OB² = AO² – AB² = 85² – 40² = 5625 = 75² или
OB = 75 (единиц).
треугольник АВН подобен треугольнику ЕВК по двум равным углам, уголАВН-общий, уголАНВ=уголЕКВ как соответственный, ВК/ВН=ЕК/АН, 4х/7х=ЕК/28, ЕК=4х*28/7х=16, ЕФ=ЕК+КФ=16+14=30