1.Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Решение.
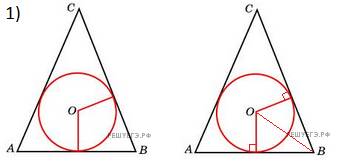
Треугольники HOBи KOB равны, т. к. являются прямоугольными с общей гипотенузой и равными катетами, значит, HB=KB=3
PABC=AC+CB+AH+HB=2CB+2HB=16+6=22
ответ: 22
2. В равнобедренный треугольник АВС с основанием ВС вписана окружность. Она касается стороны АВ в точке М. Найдите радиус окружности, если АМ = 8 и ВМ = 12.
S=1/2p*r
r=2s/p
Т.к треугольник ABC-равнобедренный, то AB=AC=30
По свойству касательных: АМ=АЕ=8, СЕ=СК=12,ВМ=КВ=12,значит ВС=24
По формуле Герона S треугольник = в корне p(p-a)(p-b)(p-c)
дано: треугольникabc=треугольникpqr
ab= 5см,bc= 6см,ac=7см решение: треугольники равны,равны все и соответсвующие стороны и углы. pq = ab = 5см,qr=bc=6см,pr = ac = 7см ответ: pq = 5см,qr = 6см,pr=7см.
ав=8
вс=?
если радиус умножить на 2 , то получится диагональ ас
вс найдем по теореме Пифагора вс²=ас²-ав² вс²=17²-8² (17 это диагональ , 8,5*2=17)
вс²=225 вс=15
подставим в формулу S=15*8=120
ответ: 120