Відповідь:
3 см
Пояснення:
Відомо, що коло, вписане в трикутник, точками дотику до сторін відділяє рівні відрізки зі сторони кожної вершини.
Також відомо, що висоти - радіуси, проведені із центра такого кола в прямокутному трикутнику до катетів утворюють з відрізками від точок дотику до вершини прямого кута квадрат зі стороною, рівною радіусу вписаного кола.
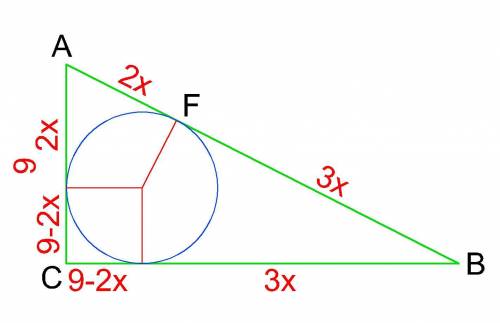
Згідно з умовою, позначимо AF як 2x, FB як 3x, тоді
r=9-2x
За теоремою Піфагора складемо рівняння:
9²+ (9-2х+3х)²=(2х+3х)²
81+(9+х)²=25х²
81+81+18х+х²-25х²=0
24х²-18х-162=0
4х²-3х-27=0
Дискрімінант: Д=9+4*4*27=441=21²
х₁=(3+21)/8=3 см
х₂=(3-21)/8=-2.25 см (не підходить).
Тоді r=9-2·3=3 см
Пусть х - длина другого катета, тогда использя свойство катета , лежащего против угла в 30 град и теоремы Пифагора, сот уравнение:
144+х2=4х2, где х2 - это х в квадрате
3х2=144
х2=48
х=4корня из 3 - другой катет.
Теперь рассмотрим маленький треугольник с тем же прямым углом и биссектрисой, которая является гипотенузой, используя тоже свойство катета и опять т Пифагора сост уравнение, в котором х - длина биссектрисы:
(х2)/4+48=х2 домножаю на 4
х2+192=4х2
3х2=192 делим на 3
х2=64
х=8 это и естьдлина биссектрисы.
Значит, смежный с ним угол САВ=180°-140°=40°.
АD - биссектриса и делит угол САВ пополам.
Угол САD=20°
Сумма острых углов прямоугольного треугольника 90°
∆ СDA- прямоугольный, ⇒
∠СDA=90°-∠CВD=70°
Для Δ BAD угол СВD - внешний и равен сумме двух внутренних, не смежных с ним. ⇒
∠DBA=70°-∠DAB=70°-20°=50°
∠ADB=180°-CDA=110°
∠DAB=20°