Если в прямоугольнике АВСD, длинные стороны ВС и АD,и провести диагональ АС, середину его обозначить точкой О,то при проведении перпендикуляра к АС в точке О получим пересечение ВС в точке Е. Проведем АЕ. Треугольники АЕО и СЕО равны как прямоугольные с одинаковыми катетами.
Значит АЕ=ЕС Пусть ВЕ=х, тогда ЕС=АЕ=2*х, ВС=3*х. Из треугольника АВЕ по теореме Пифагора находим, АВ=sqrt((2*x)^2-x^2)=x*sqrt(3).
Тогда tg(угла BCA)= АВ/ВС=x*sqrt(3)/(3*х)=sqrt(3)/3, угол ВСА равен 30 град.
Так как в прямоугольнике все углы 90 град, то
90-30= 60 град
ответ угол прямоугольника будет разделен на углы 30 и 60 град
S бічної поверхні = 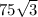 сантиметрів квадратних
сантиметрів квадратних
Объяснение:
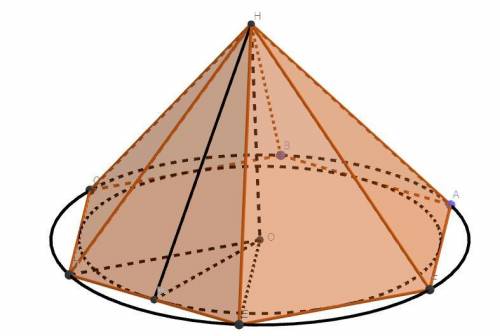
Дано: Правильна шестикутна піраміда, R = 5 см, α = 30°(α - бічні грані правильної шестикутної піраміди нахилені до основи під кутом α)
Знайти:
S - ?(площу бічної поверхні)
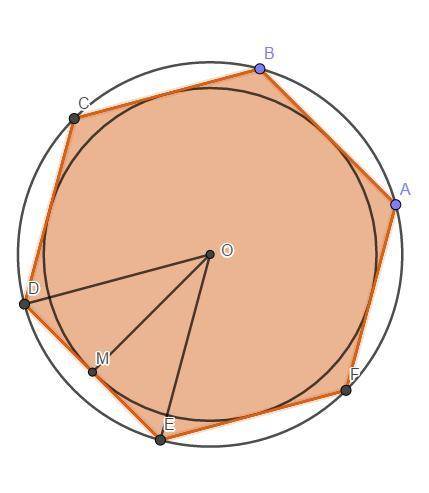
Розв'язання: Розглянемо правильний шестикутник ABCDEF. Проведемо відрізки OD і OE і розглянемо трикутник Δ DOE, який буде рівнобедренним тому, що OD = OE (OD = OE = 5см за умовою), як радіуси описаного кола.Позначимо середину відрізка DE у точці M і з вершини O проведемо відрізок OM - який буде медіаною. За умовою ∠HMO = α.За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, а так як OM⊥DE, то OM є радіусом вписаного кола.У правильного шестикутника 6 сторін, а отже шість центральних кутів, нехай центральний кут β, тоді ∠DOE = β, усі 6 центральних кутів утворють повне коло отже ∠DOE = β = 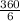 = 60°.
= 60°.
Так як OM - бісектриса за властивістю рівнобедренного трикутника, то
∠DOM = ∠MOE = ∠DOE : 2 = 60° : 2 = 30°.OM є висотою, тоді
sin ∠MOE = 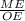 ⇒ ME = OE * sin ∠MOE = 5 * 0,5 = 2,5 см.Так як за OM - медіана, то DE = 2DM = 2ME = 2 * 2,5 = 5 см.
⇒ ME = OE * sin ∠MOE = 5 * 0,5 = 2,5 см.Так як за OM - медіана, то DE = 2DM = 2ME = 2 * 2,5 = 5 см.
cos ∠MOE =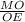 ⇒ MO = cos ∠MOE * OE = cos 30° * OE =
⇒ MO = cos ∠MOE * OE = cos 30° * OE = 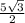 =
= 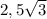
Проведемо відрізок OH - який буде висотою за властивісью шестикутної піраміди.РозглянемоΔ MOH.
cos ∠MOH = cos α = 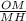 ⇒ MH =
⇒ MH = 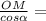
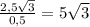 .
.
За властивістю правильної піраміди усі її грані є рівними рівнобедренними трикутниками, отже Δ HDE - рівнобедренний.Проведемо відрізок HM - який є медіаною так як DM = ME, За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, отже 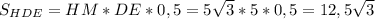 .
.
S бічної поверхні = 6 * 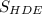 =
= 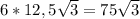 .
.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежашего кактета к прилежащему.
Значит,
ответ: 14,9 см