А1.по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов квадрат гипотенузы равен 3^2+4^2=25
гипотенуза равна корень(25)= 5 см
ответ: 5 см
А2.вводим переменную x
2x-одна сторона
3x-смежная с ней
сторона MK равна 2x а сторона KP 3x гипотенуза 5
по теореме Пифагора a²+b²=c²
(2x)²+(3x)²=5
4x²+9x²=5
13x²=5
x²=5÷13
x=√5÷13
меньшая сторона 2x =2×√5÷13
А3.Внутренний угол C=180-150=30
Тут 2 случая:
1). В=90
Пусть АВ =х . Катет, лежащий против угла 30 градусов равен половине гипотенузы:
Значит, АС= 2х
Тогда 2х=х=4; х=4
ответ: АВ=4
2).А=90
Пусть АВ =х . Катет, лежащий против угла 30 градусов равен половине гипотенузы:
Значит, ВС= 2х
Тогда 2х=х=4; х=4
ответ: АВ=4
А4.рассмотрим ΔВОС. в нем ОВ=6/2=3
ОС=8/2=4 т.к диагонали делятся пополам в месте пересечения
∠ВОС=90°, т.к диагонали перпендикулярны по св-ву.
ВС-? , ⇒
по т пифагора
ВС²=ОВ²+ОС²
ВС²=9+16
ВС²=25
ВС=5
5) Периметр квадрата со стороной AM равен 4AM.
4AM=2BC <=> AM=BC/2
Отрезок из прямого угла к гипотенузе, равный ее половине - медиана.
AM - медиана и высота, следовательно △ABC - равнобедренный, острые углы 45.
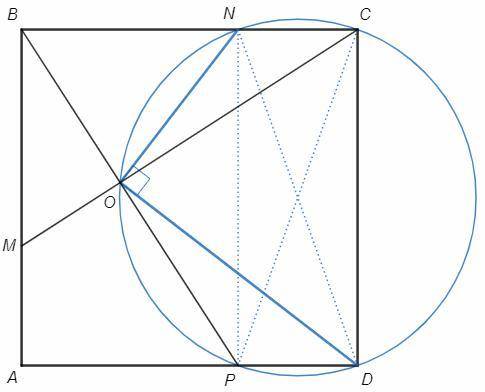
6) Продолжим перпендикуляр BO до пересечения с AD в точке P.
OBM= 90-OMB =BCM
△ABP=△BCM (по катету и острому углу)
AP=BM=BN => PD=NC
PNCD - прямоугольник, диагонали являются диаметрами описанной окружности.
COP=90, точка O лежит на окружности с диаметром CP.
Вписанный угол NOD опирается на диаметр ND, NOD=90