АВ и АС -отрезки касательных, проведенных из точки А к окружности с центром О. Найти АВ и АС, если АО=20 см, ∠ ВОС= 120.°
Объяснение:
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания, значит ∠ОВА=∠ОСА=90.
По свойству отрезков касательных АВ=АС .∠ОАВ=∠ОАС.
ΔОАВ=ΔОАС , как прямоугольный по гипотенузе и острому углу : АО -общая, ∠ОАВ=∠ОАС. В равных треугольниках соответственные элементы равны :∠ВОА=∠СОА=60°
ΔАВО-прямоугольный ,ОА=20 , sin60°=ВА/ОА , √3/2=ВА/20
ВА=10√3 .Значит ВА= АС=10√3 см.
5) Периметр квадрата со стороной AM равен 4AM.
4AM=2BC <=> AM=BC/2
Отрезок из прямого угла к гипотенузе, равный ее половине - медиана.
AM - медиана и высота, следовательно △ABC - равнобедренный, острые углы 45.
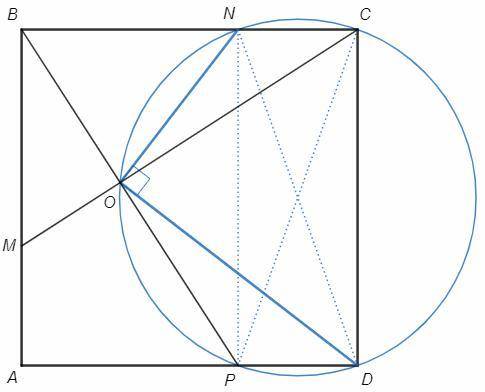
6) Продолжим перпендикуляр BO до пересечения с AD в точке P.
OBM= 90-OMB =BCM
△ABP=△BCM (по катету и острому углу)
AP=BM=BN => PD=NC
PNCD - прямоугольник, диагонали являются диаметрами описанной окружности.
COP=90, точка O лежит на окружности с диаметром CP.
Вписанный угол NOD опирается на диаметр ND, NOD=90
По формуле C=2π·R
R=C:2π=19,8 дм:6,28=
2) сторону треугольника найти из прямоугольного треугольника СОК. К- основание высоты ВК.
2√27=6√3
Сторона квадрата 6√3, значит его диагональ 6√3·√2=6√6
Радиус описанной окружности равен половине диагонали 3√6