 с прямым углом
с прямым углом  , EF — биссектриса
, EF — биссектриса  ,
,  , FG — искомый отрезок.
, FG — искомый отрезок.  .
.  — биссектриса, то
— биссектриса, то  (биссектриса
(биссектриса  делит
делит  на два равные угла).
на два равные угла). 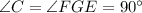 (это следует из условия: так как
(это следует из условия: так как  прямоугольный, то и
прямоугольный, то и  ; так как
; так как  — расстояние от
— расстояние от  до
до 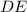 , то
, то 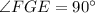 ).
).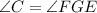 и
и 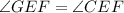 , то и третий угол первого треугольника равен третьему углу второго треугольника:
, то и третий угол первого треугольника равен третьему углу второго треугольника:  . Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так:
. Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так: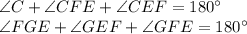
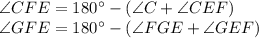
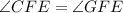 .
.  является для обоих треугольников общей.
является для обоих треугольников общей. (второй признак равенства треугольников — по стороне и двум прилежащим к ней углам (
(второй признак равенства треугольников — по стороне и двум прилежащим к ней углам ( — сторона, а
— сторона, а  — два прилежащих угла)).
— два прилежащих угла)). соответствует
соответствует  , тогда:
, тогда: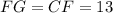
 . Смотрите второй рисунок.
. Смотрите второй рисунок.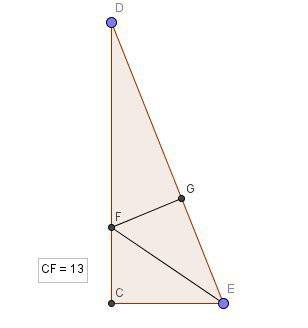
Если опустить перпендикуляры из B и C на AD, пусть это будут BH1 и CH2, то мы получим два равных треугольника ABH1 и CH2D (равны по углам A и D и гипотенузе тк трапеция равнобедренная. Тогда AH1=H2D => AD= AH1+H1H2+H2D=2AH1+H1H2
H1H2 будет равно BC (если надо будет объяснить почему - объясню).
В треугольнике прямоугольном AH1B угол BAH1 будет равен 60 т.к. АС биссектриса и угол CAH1 равен 30 (все по условию). Значит по свойству (если катет в прямоугольном треугольнике лежит портив угла в 30 градусов (угол ABH1=30) то он равен половине гипотенузы) AB=2AH1=CD
рассмотрим треугольник ACD он будет прямоугольным с прямым углом ACD тк CAD=30, ADC=60 тогда по св-ву, описанному выше, CD=AD/2=4 и тогда можно найти AH1=AB/2=2
периметр равен сумме сторон
P=AB+BC+CD+AD где AB=CD=4, BC=AD-2AH1=8-4=4
подставим в P => P=8 + 4 + 4 =16
ответ 16
2) Периметр равен удвоенной сумме длины одной стороны и другой
P=2*(a+b)
P-a=23 => a=P-23
P-b=19 => b=P-19
тогда подставим и получим P= 2*( P-23 + P-19)
P=2P -46 + 2P-38
3P=84 => P=28
ответ 28