Пусть S₁ - это площадь бо́льшего треугольника, а S₂ - площадь меньшего треугольника.
Пусть k > 1 (это значит, что в числителе будет стоять бо́льший треугольник).
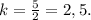
Отсюда -
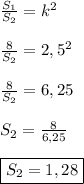
1,28 (ед²).
- - -
Случай 2 - Площадь меньшего треугольника равна 8 (ед²).В этом случае наоборот k < 1 (в числителе будет стоять меньший треугольник).
S₁ - площадь бо́льшего треугольника, S₂ - площадь меньшего треугольника
Тогда -
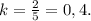
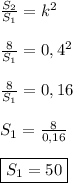
50 (ед²).
Длина двух сторон равнобедренного треугольника составляет 5 см и 7 см. Какой может быть периметр этого треугольника?
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Решение :Равнобедренный треугольник - это такой треугольник, две стороны которого равны между собой.Для выполнения задания также необходимо учесть и неравенство треугольника (каждая сторона треугольника меньше суммы двух других сторон).
Допустим, что основание равно 5 см, тогда боковые стороны равны по 7 см.
"Проверяем" каждую сторону -
7 см + 7 см > 5 см - верное неравенство.
7 см + 5 см > 7 см - верное неравенство.
7 см + 5 см > 7 см - верное неравенство.
Как видим, все неравенства верны, следовательно, такой треугольник существует. Тогда его периметр (сумма длин всех сторон) равен 5 см + 7 см + 7 см = 19 см.
Теперь допустим, что основание равно 7 см, тогда боковые стороны равны по 5 см.
Аналогично -
5 см + 5 см > 7 см - верное неравенство.
7 см + 5 см > 5 см - верное неравенство.
7 см + 5 см > 5 см - верное неравенство.
Неравенства верны, треугольник существует. Тогда его периметр равен 5 см + 5 см + 7 см = 17 см.
ответ : 19 см и 17 см.
Найдем линию пересечения плоскостей АВС и ВЕD1, к которой надо провести перпендикулярную плоскость.
Для начала построим сечение BED1.
Точки Е и В лежат в грани АA1В1В, следовательно ЕВ - линия пересечения этой грани и секущей плоскости.
Точки Е и D1 лежат в грани АA1D1D, следовательно ЕD1 - линия пересечения этой грани и секущей плоскости.
Зная, что параллельные плоскости пересекаются третьей плоскостью по параллельным прямым, проводим ВР параллельно ED1 и D1Р параллельно ЕВ. Параллелограмм ВЕD1P - искомое сечение.
Продлив прямую D1E до пересечения с продолжением ребра DA, получим точку F, принадлежащую и плоскости АВС (прямая AD принадлежит плоскости АВС) и секущей плоскости BED1 (D1E принадлежит плоскости BED1). Линия пересечения плоскостей BED1 и АВС проходит через точку В (дано). Поэтому, соединив точки F и В получим искомую линию пересечения.
Теперь проведем плоскость, перпендикулярную этой линии пересечения.
Для этого опустим перпендикуляр АН на FB. Плоскость AFH - искомая плоскость, так как прямая ЕА перпендикулярна плоскости АВС, а прямая ЕН перпендикулярна FB по теореме о трех перпендикулярах (АН - проекция наклонной ЕН).
Искомый угол между плоскостями - это <AHE (по определению).
Треугольник AFE подобен треугольнику DFD1 с коэффициентом подобия k=AE:DD1=1:3. тогда AF/FD=AF/(AF+AD)=AF/(AF+2)=1/3.
Отсюда AF=1. В прямоугольном треугольнике AFB (<A=90 - дано) по Пифагору FB=√(AF²+AB²)= √(1+4)=√5. АH=AF*AB/FB (свойство высоты из прямого угла). АH=1*2/√5 = 2/√5.
Тангенс искомого угла равен
tg(AHE)=AE/AH = 1/(2/√5) = √5/2 ≈1,12
ответ: α = arctg(1,12) ≈ 48,2°.