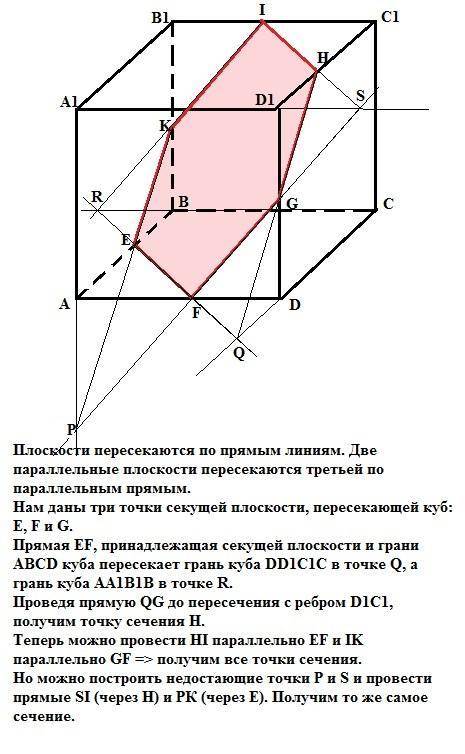
Сечение - правильный шестиугольник.
Объяснение:
Плоскости пересекаются по прямым линиям. Две параллельные плоскости пересекаются третьей по параллельным прямым.
Нам даны три точки секущей плоскости, пересекающей куб: E, F и G, расположенные на ребрах АВ, AD и DD1 соответственно.
Прямая EF, принадлежащая секущей плоскости и грани АВСD куба пересекает грань куба DD1C1C в точке Q, а грань куба AA1B1B в точке R.
Проведя прямую QG до пересечения с ребром D1C1, получим точку сечения Н.
Теперь можно провести НI параллельно EF и IK параллельно GF => получим все точки сечения.
Но можно построить недостающие точки P и S (построение понятно из рисунка) и провести прямые SI (через Н) и РК (через Е). Получим то же самое сечение, которое в силу симметричности точек является правильным шестиугольником.
Объяснение:
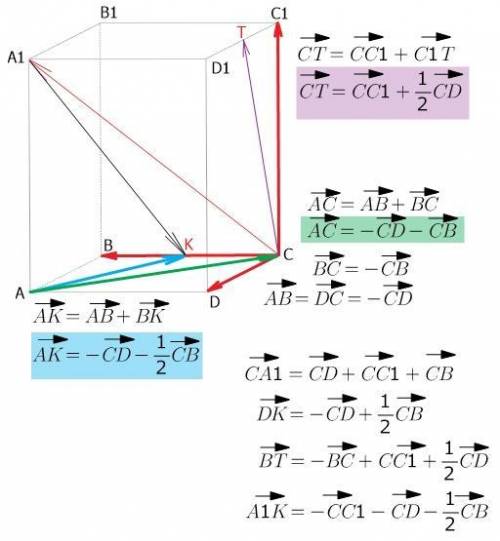
Вектор -это направленное перемещение.
чтобы разложить векторы по указанным векторам, можно представлять, что "как будто вы вышли из вершины А и идете по ребрам призмы в вершину С и записываете свой путь"...
из точки А могу "пройти" в точку В (это вектор АВ); из В могу "пройти" в точку С (это вектор ВС)...
но перемещение из А в В (вектор АВ) по длине в точности равно
перемещению из С в D (вектору CD), только направление в другую сторону... направление "показывает" знак "минус"
вектор АВ = вектору DC
вектор DC = "минус" вектор CD
треугольник АВС, АВ=ВС=48, радиус описанной=25=ВС/(2*sinA), 25=48/(2*sinA), sinA=24/25, cosA=корень(1-sinA в квадрате)=корень(1-576/625)=7/25, проводим высотуВН=медиане
треугольник АВН прямоугольный, АН=НС=АВ*cosA=48*7/25=13,44, АС=2*АН=2*13,44=26,88