по т косинусов найду BD
BD^2=AB^2-AD^2-2*AB*AD*cos<A=7^2+15^2-2*7*15*0.5=274-105=169=13^2
BD=13
У вписанного четырехугольника суммы противоположных углов 180 °
<C=180-<A=180-60=120°
Тогда по той же теореме выражу BD из ΔBCD
BD^2=BC^2+CD^2-2*BC*CD*cos<C
169=(x+1)^2+x^2-2x(x+1)*cos120
169=x^2+2x+1+x^2-2x(x+1)(-0.5)
169=2x^2+2x+1+x^2+x
169=3x^2+3x+1
3x^2+3x-168=0-делю на 3
x^2+x-56=0
D=1+224=225=15^2
x=(-1+15)/2=7
Тогда CD=7;BC=8
S(ABD)=0.5AB*AD*sin<A=0.5*7*15*√3/2=105√3/4
S(BCD)=0.5*BC*CD*sin<C=0.5*8*7*sin120=56√3/4
S(ABD)/S(BCD)=105/56
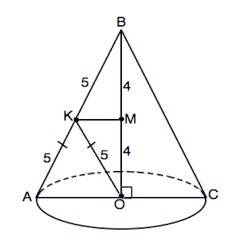
Осевое сечение конуса- равнобедренный треугольник АВС.
Расстояние от центра основания конуса до середины образующей является медианой ОК прямоугольного треугольника АВО, где ВО - высота конуса, АО - радиус основания, АВ- образующая.
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине.
Следовательно, АВ=2•КО=10 см.
Отношение катета ВО к гипотенузе АВ равно 8:10=4:5, т.е. ∆ АВО египетский, следовательно,
радиус основания конуса АО=6 см ( можно проверить по т.Пифагора с тем же результатом).