Периметр ромба P = 68 см
площадь ромба равна 240 см квадратных
Объяснение:
Ромб — это параллелограмм, у которого все стороны равны.
Периметр ромба P=4a = 4* 17 = 68 см
Если одна диагональ 30 см, то она образует с другой диагональю прямоугольный треугольник, с гипотенузой 17 см, и катетом 30/2 = 15 см.
второй катет равен корню из разности квадрата гипотенузы и квадрата известного катета = 8 см. Этот катет равен половине второй диагонали. Диагональ 2*8 = 16 см.
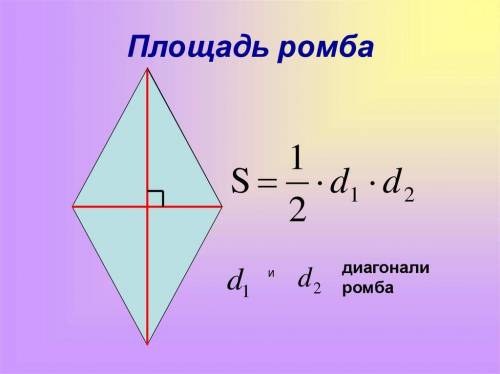
Следовательно площадь ромба равна (16*30)/2 = 240 см квадратных
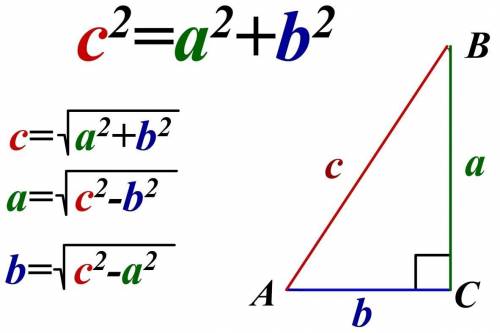
Объяснение:
25) выпуклом четырёхугольнике градусная мера трех углов соответственно равны 60°, 80° и 100° . Найдите четвёртый угол.
26) Сумма трех углов выпуклого четырехугольника равна 300° . Найдите четвёртый угол.
25) сумма углов многоугольника находится по формуле Σ=180°×(n-2) где n- число сторон, углов многоугольника.
Σ=180°×(4-2)=180°×2=360°
Обозначим четвёртый угол как Х.
60°+80°+100°+Х=360°
240°+Х=360°
Х=360°-240°
Х=120° четвёртый угол равен 120°
26) сумма всех четверых углов четырехугольника 360°
Сумма трёх углов 300°
Четвёртый будет
360°-300°=60°
Площадь диагонального сечения будет равна произведению высоты параллелепипеда и диагонали ВD основания.
Чтобы найти вторую диагональ основаняи, вспомним, что сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов длин сторон.
D²+d² =2(a²+b²)
Отсюда
d²=2(a²+b²)-D²
d²=2(3²+4²)-6²
d²=2(9+16)-36
ВD=√14
S=14·√14 м²