1 - 21 градусов
(180 градусов - 32 градуса) : 2= 74 градуса- углы А и С
74 градуса : 2= 37 градусов - угол А разделен биссектрисой АN
Рассмотрим прямоугольный треугольник AMC
90 градусов - 74 градуса= 16 градусов - угол MAC
угол NAC - угол MAC= 37 градусов - 16 градусов = 21 градус
2 - BR < AB < BT
угол Т= 30 градусов, поэтому катет, что находится напротив угла 30 градусов равен половине гипотенузы. В нашем случае BR=1/2 BT
Рассмотрим треугольник ABR. BR < AB так как гипотенуза всегда больше за катет.
Поэтому ответ BR < AB < BT
Пусть AC=x, тогда в ΔABC по формуле Герона:
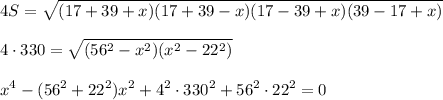
Решим квадратное уравнение относительно x².
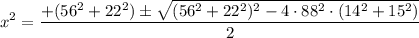
Далее немного вычислений, и зная, что x>0, как сторона треугольника, получим:
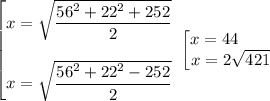
Пусть KL=a, KN=b.
Рассмотрим случай, когда AC=44.
В ΔABC по теореме косинусов:
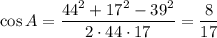
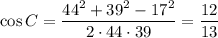
По формуле связи косинуса и тангенса:
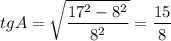
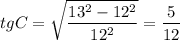
В прямоугольных треугольниках AKL и CNM выразим AK и CN через a, основываясь на определении тангенса острого угла в прямоугольном треугольнике.
AK=8a/15; CN=12a/5
AC=AK+KN+NC=(44a/15)+b=44
P(KLMN)=2a+2b=59
Составим систему и определим S(KLMN)=ab
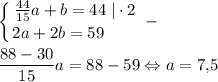
b=(59-15)/2=22
ab=7,5·22=165
Теперь всё тоже самое только AC=2√421.
В ΔABC по теореме косинусов:
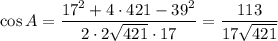
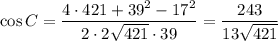
По формуле связи косинуса и тангенса:
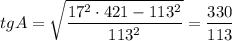
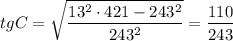
AK=113a/330; CN=243a/110
AC=AK+KN+NC=(421a/330)+b=2√421
P(KLMN)=2a+2b=59
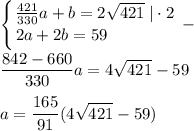
Заметим, что проекция AB на AC равна AB·cosA=113/√421
Получается, что AK=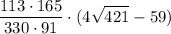 > 113/√421.
> 113/√421.
Таким образом при АС=2√421 картинка другая, которая не удовлетворяет условию задачи.
ответ: 165.