Пирамида
Пирамидой называется многогранник, поверхность которого состоит из многоугольника, называемого основанием пирамиды, и треугольников с общей вершиной, называемых боковыми гранями пирамиды. Пирамида называется n-угольной, если ее основанием является n-угольник.
Пирамида называется правильной, если её основание — правильный многоугольник и все боковые ребра равны.
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию. Усечённая пирамида называется правильной, если пирамида, из которой она была получена — правильная.
Тетраэдром называется треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды. Кроме того, существует большое различие в
Объяснение:
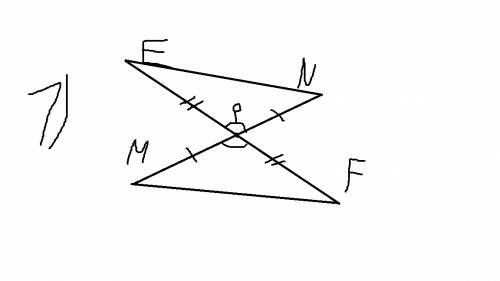
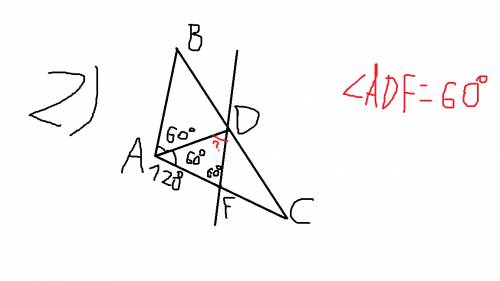
пирамида КАВС, К-вершина АВС-прямоугольный треугольник, уголС=90, уголА=60, уголВ=90-60=30, ВС=12, АВ=ВС/sin60=12/(корень3/2)=8*корень3, АС=1/2АВ=8*корень3/2=4*корень3, высота КН на АВ, точка Н - центр описанной окружности находится на середине гипотенузы АВ, КА=КС=КВ=13, АН=ВН=1/2АВ=8*корень3/2=4*корень3,
треугольник АКН прямоугольный, КН-высота пирамиды=корень(АК в квадрате-АН в квадрате)=корень(169-48)=11
площадьАВС=1/2*АС*ВС=1/2*4*корень3*12=24*корень3
объем=1/3*площадьАВС*КН=1/3*24*корень3*11=88*корень3