Грань АА1С1С - квадрат.
АС по т.Пифагора равна 20. В призме все боковые ребра равны. ⇒ ВВ1=СС1=АА1=АС=20.
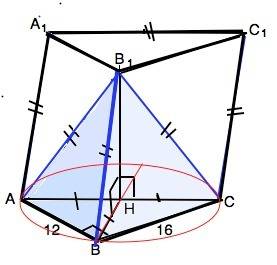
По условию боковые ребра пирамиды АВ1СВ равны, значит, их проекции равны между собой и равны радиусу окружности, описанной около основания АВС. ⇒
Вершина пирамиды В1 проецируется в центр Н описанной около прямоугольного треугольника окружности, т.е. лежит в середине гипотенузы.
∆ АВС прямоугольный, R=АС/2=10.
АН=СН=ВН=10.
Высота призмы совпадает с высотой В1Н пирамиды.
По т.Пифагора
В1Н=√(BB1²-BH²)=√(20²-10²)=√300=10√3
Формула объёма призмы
V=S•h где S - площадь основания, h - высота призмы.
S-12•16:2=96 (ед. площади)
V=96•10√3=960√3 ед. объёма.
SO - высота пирамиды, ОС - проекция SC на плоскость основания, значит ∠SCO - угол наклона бокового ребра к плоскости основания - искомый.
ОС - радиус окружности, описанной около правильного треугольника:
ОС = АВ√3/2 = 6√3/3 = 2√3.
ΔSOC: ∠SOC = 90°, ctg∠SCO = OC / SO = 2√3 / 8 = √3/4
2. Основание правильной четырехугольной пирамиды - квадрат, боковые грани - равнобедренные треугольники.
Пусть Н - середина CD, тогда SH - медиана и высота равнобедренного треугольника SDC, ОН - средняя линия ΔADC, ⇒ ОН║AD, ⇒ OH⊥CD.
Значит ∠SHO - линейный угол двугранного угла наклона боковой грани к основанию - искомый.
Радиус окружности, описанной около квадрата, равен половине его диагонали, значит АС = 8.
АС = АВ√2 ⇒ АВ = АС/√2 = 8 / √2 = 4√2 - сторона квадрата
ОН = AD/2 = 2√2
ΔSOH: ∠SOH = 90°, cos∠SHO = OH / SH = 2√2/7
3. Sбок = 2πRH = 160π см² ⇒ 2RH = 160 см²
ABCD - осевое сечение.
Sabcd = 2R·H = 160 см²
ABEF - сечение, параллельное оси и отстоящее от нее на 6 см.
Так как H = R - 2,то
2R(R - 2) = 160
R² - 2R - 80 = 0
D = 4 + 320 = 324
R = (2 + 18)/2 = 10 см R = (2 - 18)/2 = - 8 - не подходит по смыслу задачи
H = 10 - 2 = 8 см
Если Н -середина ВЕ, то ОН = 6 см - расстояние от оси до сечения.
ΔОНВ: ∠ОНВ = 90°, по теореме Пифагора
НВ = √(ОВ² - ОН²) = √(100 - 36) = 8 см
ВЕ = 2НВ = 16 см
Sabef = BE · H = 16 · 8 = 128 см²
4. ΔАВС - данное сечение - равнобедренный треугольник (АВ = АС = l образующие)
∠АВС = ∠АСВ = 75°, ⇒ ∠ВАС = 30°.
Sabc = 1/2 · AB · AC · sin ∠BAC = 16 см²
l² · sin30° = 32
l² = 64
l = 8 cм
ΔАОВ: ∠ВАО = 30° по условию.
cos∠BAO = AO/AB
cos30° = h/l ⇒ h = l · cos30° = 8√3/2 = 4√3 см
r = OB = AB · sin30° = 8 · 1/2 = 4 см
Площадь осевого сечения:
Sakc = 1/2 · KC · AO = r · h = 16√3 см²
Sполн = πr(l + r) = π · 4 · (8 + 4) = 48π см²