ответ: 3 (ед. площади)
Объяснение:
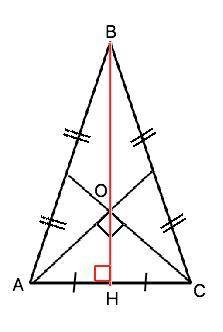
Пусть данный треугольник АВС; АВ=ВС, АС=2. О - точка пересечения медиан; угол АОС=90°
Медианы равнобедренного треугольника, проведенные к боковым сторонам, равны. Проведем третью медиану из вершины В. ОН - медиана и высота прямоугольного равнобедренного треугольника АОС и равна половине гипотенузы АС.(свойство) ОН=АС:2=1. Медианы треугольника пересекаются в одной точке и делятся при этом в отношении 2:1, считая от вершины.⇒ Высота ВМ=ВО+ОН=3•ОН=3. Площадь ∆ АВС=ВН•АС:2=3•2:2=3 (ед. площади).
Можно применить свойство медиан делить треугольник на равновеликие части. Ѕ(АОВ)=Ѕ(ВОС)=Ѕ(АОС) Поэтому Ѕ(АВС)=3•Ѕ(АОС). Вы сможете сделать это самостоятельно.
Она будет равна 13 тк 169=144+25
Найдем длину бокового ребра
Если говорится что диагональ равна 13 корней из двух то по теореме Пифагора боковое ребро рано тоже 13 тк 13 корней из 2 в квадрате это 13 в квадрате +13 в квадрате
Тогда площадь оснований равна (5*12/2)*2=60
Площадь боковой поверхности равна (5+12+13)*13=390
Тогда полная площадь равна 390+60=450 квадратных дециметров
ответ : 450 квадратных дециметров)