Так как BL – биссектриса угла ABC, то ∠ABL = ∠LBC. Поскольку PB – касательная к Ω, то ∠PBA = ∠BCA. Кроме того,
∠PBL = ∠PBA + ∠ABL = ∠BCA + ∠LBC = ∠BLP, значит, ∠BPM = 180° – (∠PBL + ∠BLP) = 180° – 2∠BLP. Отсюда следует, в частности, что угол BLP – острый.
Так как ∠BLM = 180° – BLP > 90°, касательные к Γ в точках B и M пересекаются в точке Q, лежащей по ту же сторону от BM, что и точка L (а значит – по ту же сторону, что и P). Далее имеем ∠QBM = ∠QMB = 180° – ∠BLM = ∠BLP. Значит, ∠BQM = 180° – 2∠QBM = 180° – 2∠BLP = ∠BPM. Поэтому точки B, M, P и Q лежат на одной окружности. Отсюда следует, что ∠QPM = ∠QBM = ∠BLP. Это и означает, что PQ || BL.
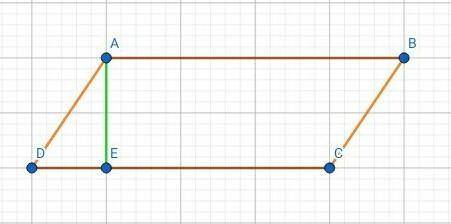
Параллелограмм.
CD = 12 см
AD = 3√3 см
∠ADC = 60˚
Найти:S - ?
Решение:Проведём высоту АЕ.
△DAE - прямоугольный, так как АЕ - высота.
"Сумма острых углов прямоугольного треугольника равна 90°".
=> ∠DAE = 90˚ - 60˚ = 30˚
"Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы".
=> DE = 3√3/2 см.
"Если угол прямоугольного треугольника равен 60°, то напротив лежащий катет равен произведению меньшего катета на √3".
=> AE = 3√3/2 * √3 = 9/2 = 4,5 см
S = CD * AE = 12 * 4,5 = 54 см²
ответ: 54 см²