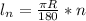, где n - градусная мера соответственного центрального угла.
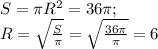, где S - площадь круга.
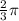см.
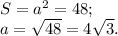
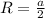, где a - сторона квадрата.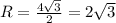
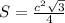, где c - сторона правильного треугольника.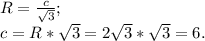
.
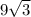см.
80 см^2
Объяснение:
Рассмотрим треугольник , лежащий в основании.АВ=ВС=10 и АС=12
BD -биссектриса угла В. Так как треугольник равнобедренный, то
BD^2= AB^2 - (AC/2)^2 = 100-36=64
BD=8
О-точка пересечения биссетрис . Тогда по свойству биссектрисы:
ВО:ОD= AB:AD=10:6 =5:3
Значит ВО=5 см OD=3 см
Пусть вершина пирамиды S
Тогда SB^2= BO^2+OS^2= 25+16=41
SB=sqr(41)
Теперь найдем АО^2=ОС^2= AD^2+OD^2= 36+9=45
SA^2=SC^2= AO^2+OS^2= 45+16=61
SA=sqr(61)
Найдем площадь треугольника ACS :
Высота этого треугольника SD= sqr (SA^2-AD^2)=sqr(61-36)=5
Sasc=AC*SD/2=12*5/2=30
Найдем площадь треугольника ACB : AF и BF- отрезки , на которые высота делит сторону АВ. AF=6 , BF=4
Высота этого треугольника = sqr (SA^2-AF^2)=sqr(61-36)=5
Sasb=AB*SF/2=10*5/2=25
Заметим, что треугольники ASB = CSB=25
Тогда полная площадь боковой поверхности:
25+25+30=80
