Вромбе авсд бессекстриса угла вас пересекает сторону вс и диагональ вд соответственно в точках м и n, угол амс= 120 градусов. найдите величину угла anb.

👇

Увидеть ответ

Ответ:

tar02

16.05.2022

Стороны ромба равны. => ∆ АВС - равнобедренный, угол ВАС=ВСА.

Примем угол МАС, половину угла ВАС, равным а.

Тогда угол МСА=ВАС=2а.

Из суммы углов треугольника ∠МАС+∠МСА+∠АМС=180° ⇒

а+2а=180°-120°=60°

а=20°

Диагонали ромба пересекаются под прямым углом.

∆ АОN- прямоугольный.

угол АNO=180°-90°-20°=70°

Искомый угол ANB смежный углу ANO, их сумма 180°

Угол ANB=180°-70°=110°

Вромбе авсд бессекстриса угла вас пересекает сторону вс и диагональ вд соответственно в точках м и n

4,6(76 оценок)

Открыть все ответы

Ответ:

Rustamka45

16.05.2022

Площадь равнобедренной трапеции равна полусумме оснований, умноженной на высоту.

Высота у нас уже есть Одно из оснований - тоже. Теперь надо найти большее основание. Если опустить высоту с меньшего основания на большее, то получим прямоугольный треугольник, где гипотенузой будет боковая сторона, одним из катетов - высота трапеции, а вторым катетом - часть основания трапеции. Чтобы узнать большее основание трапеции, нам нужно вычислить этот неизвестный катет в треугольнике, потому что длиной большего основания будет сумма двух таких катетов с меньшим основанием. Так как точно такой же треугольник можно получить, опустив высоту из другой точки меньшего основания трапеции. По теореме Пифагора вычисляем неизвестный катет 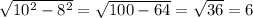$\sqrt{10^2-8^2}=\sqrt{100-64}=\sqrt{36}=6$ . Значит длина наибольшего катета равна 7+6+6=19 см.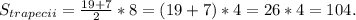 $S_{trapecii}=\frac{19+7}{2}*8=(19+7)*4=26*4=104.$

4,5(4 оценок)

Ответ:

Gay1122

16.05.2022

Точка К, из которой будет виден отрезок МN под наибольшим углом, будет находиться на общей окружности с точками М и N. При этом OK для неё является касательной.
По свойству касательной и секущей ОК²=ОМ·ОN.
Пусть ОМ=х, тогда ОN=OM+MN=x+6,
4²=x(х+6),
х²+6х-4=0,
х1=-8, отрицательное значение не подходит,
х2=2.
ON=2+6=8 дм - это ответ.

Теперь докажем, что отрезок MN виден из точки К под большим углом.
Пусть радиус окружности около тр-ка КMN равен r.
На стороне ОК в любом месте возьмём точку Р и опишем окружность около тр-ка РMN, радиусом R. ОР для неё является секущей, а для окружности, радиусом r - касательной, значит R>r.
Формула хорды: l=2R·sin(x/2), где х - градусная мера хорды.
∠MKN=α, ∠MPN=β.
Обратим внимание, что углы α и β - это половина градусной меры хорды.
MN=2R·sinβ ⇒ sinβ=MN/2R.
MN=2r·sinα ⇒ sinα=MN/2r.
Сравним синусы, предположив, что они равны.
MN/2R=MN/2r.
1/R=1/r, но R>r, значит 1/R<1/r, значит sinβ<sinα.
Так как градусная мера хорды не может быть больше 180°, значит в формуле хорды 0°<α<90°, 0°<β<90°.
В этом диапазоне синус угла тем больше, чем больше его градусная мера,
значит α>β.
Доказано.
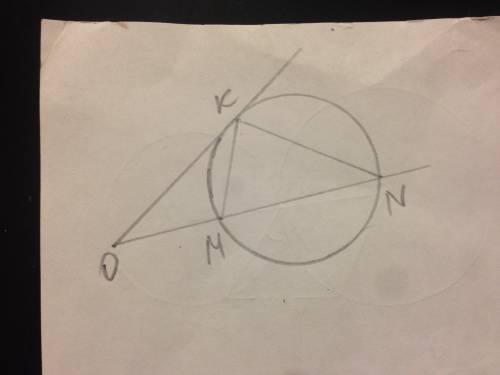
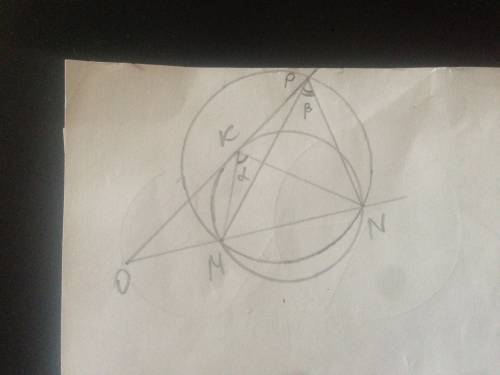
Решить на одной из сторон острого угла с вершиной о отмечены точки м и n ( м лежит между о и n). на